 Обработка растровых изображений
Обработка растровых изображений
Шумы, их свойства, методы уменьшения влияния.
Так как данный ресурс посвящен компьютерной графике, то в дальнейшем, говоря о сигнале, мы будем понимать или изображения в градации серого как однокомпонентный двумерный сигнал, или, в случае полноцветного изображения - трехкомпонентный двумерный сигнал.
В последнем случае компонентами сигнала могут быть цвета - красный (R), зеленый (G), синий (B) или хроматические составляющие Y - освещенность, Cr- теплые оттенки, Cb-холодные оттенки, или элементы пространства HSV, главные компоненты PCA пространства цветов, или компоненты другого пространства цветов.
Переходя к рассмотрению темы раздела, надо отметить, что в реальных сигналах шум так или иначе присутствует. Этот факт обусловлен как аппаратной составляющей, с помощью которой полученное изображение, так и влиянием состояния атмосферы, движением относительно объекта съёмки и др. Компоненты шума изображений могут объединяться с полезным сигналом \(s [k_1, k_2]\) адитивно: \[ f [k_1, k_2] = s [k_1, k_2] + n [k_1, k_2], \] или мультипликативно: \[ f [k_1, k_2] = s [k_1, k_2] * n [k_1, k_2]. \] Типичный пример мультипликативного взаимодействия сигнала с шумом - связь между освещенностью видеообъектива (полезный сигнал) и световым потоком, отраженным от местных объектов (шум).К аддитивных относятся, в основном, шумы, обусловленные свойствами чувствительных элементов видео или фотокамер. Эти шумы возникают по следующим причинам:
- Дефекты (примеси и др.) потенциального барьера, которые вызывают утечку заряда, сгенерированного за время экспозиции - т.н. черный дефект. Такие дефекты видно на светлом фоне в виде темных точек.
- Темновой ток (Dark current) - является вредным последствием термоэлектронной эмиссии и возникает в сенсоре при подаче потенциала на электрод. Такие дефекты видны на темном фоне в виде светлых точек, это т.н. белый дефект. Белые дефекты особенно проявляются при больших экспозициях. Основная причина возникновения темнового тока - это примеси в кремниевой пластине или повреждения кристаллической решетки. Чем чище кремний, тем меньше темновой ток. На темновой ток влияет температура элементов камеры и электромагнитные наводки. При увеличении температуры на 6-8 градусов, значение темнового тока удваивается.
- Шум, возникающий вследствие стохастической природы взаимодействия фотонов света с атомами материала фотодиодов сенсора. Во время движения фотона внутри кристаллической решетки может возникнуть ситуация, когда фотон, «попав» в атом кремния, выбьет из него электрон, породив пару электрон-дырка. Электрический сигнал, снимаемый с датчика, будет соответствовать количеству порожденных пар.
- Наличие дефектных (не работающих) пикселей, которые возникают при производстве фотосенсоров. Для устранения их негативного влияния используются математические методы интерполяции, когда вместо дефектного «подставляется» или просто соседней элемент, или среднее по прилегающим элементам, или значение, вычисленное более сложным образом. Естественно, что вычисленное значение отличается от фактического и ухудшает качество получаемого изображения.
Немного о фильтрах.
Импульсная переходная функция (impulse response) или импульсная характеристика - это отклик системы на дельта-функцию Дирака. Если рассматривать линейную систему в пространстве времени, то сигнал на выходе линейной системы \(y(t)\) можно рассчитать как свертку входного сигнала \(x ( t )\) с импульсной характеристикой \(h (t)\): \[ y(t)=h(t)\otimes x(t)=\int_{-\infty}^\infty h(\tau)x(t-\tau)d\tau. \] Для преобразования сигналов часто используются линейные системы, называемые фильтрами, передаточная функция которых (частотная характеристика) имеет определенную форму. Одни из самых используемых фильтров - это пороговые фильтры, например,-
Фильтр низких частот (low-pass filter)
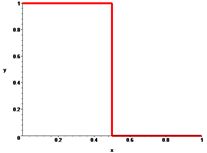
-
Фильтр высоких частот (high-pass filter)
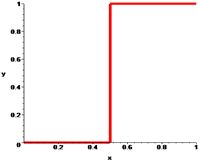
-
Полосно-пропускающий фильтр (band-pass filter)
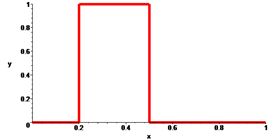
-
Полосно-ограничивающий фильтр (band-stop filter)

Препарирование изображения.
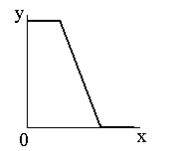
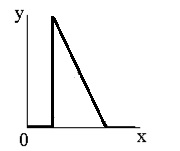
Препарирования представляет собой класс поэлементного преобразования (как правило, освещение) изображений. Характеристики применяемых на практике процедур препарирования приведены на рисунке ниже.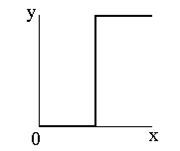 | 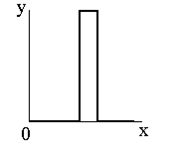 | 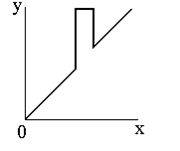 |
| а | б | в |
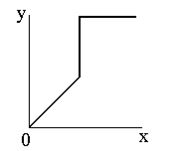 | 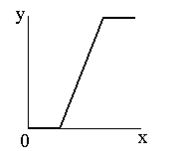 |  |
| г | д | е |
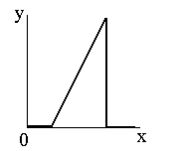 |  | 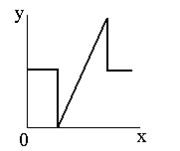 |
| ж | з | и |
Безусловно, ключевым в бинаризации является выбор порога. Существует много различных подходов к выбору порога бинаризации, но наиболее популярным является метод Оцу (? ? ? ? OtsuNobuyuki).
Идея метода Оцу заключается в том, чтобы выставить порог между классами таким образом, чтобы каждый из них был как можно более «плотным». Если выражаться математическим языком, то это сводится к минимизации внутришньокласовои дисперсии, которая определяется как взвешенная сумма дисперсий двух классов: \[ \sigma_W^2=w_1 \sigma_1^2+w_2 \sigma_2^2, \] для любого фиксированного \(k=0,1,…,255\) \[ w_1=\frac{\sum_{i=0}^kh_i}{H\times W}, \mu_1=\frac{\sum_{i=0}^kih_i}{\sum_{i=0}^kh_i}, \sigma_1=\frac{\sum_{i=0}^k(i-\mu_1)h_i}{\sum_{i=0}^kh_i}, \] \[ w_2=\frac{\sum_{i=k+1}^{255}h_i}{H\times W}, \mu_2=\frac{\sum_{i=k+1}^{255}ih_i}{\sum_{i=k+1}^{255}h_i}, \sigma_2=\frac{\sum_{i=k+1}^{255}(i-\mu_2)h_i}{\sum_{i=k+1}^{255}h_i}, \] и \(\{h_i \}_{i=0}^{255}\) -гистограма интерсивности освещения (компоненты Y).Перебираем поочередно все k=0,1,...,255 и то значение, при котором достигается минимум величины \(\sigma_W^2\) будет отвечать порогу бинаризации.
 |  |
| Оригинальное изображение Lena | Бинаризация изображения Lena методом Оцу. |
Пространственные методы обработки изображений.
Пространственные методы обработки изображений объединяют подходы, основанные на прямом манипулировании пикселями изображения. Некоторые локальные преобразования оперируют одновременно как со значениями пикселей в окрестности, так и с соответствующими им значениями некоторой матрицы, которая имеет те же размеры, что и окрестность. Такую матрицу называют фильтром, маской, ядром, шаблоном или окном. Значения элементов матрицы принято называть коэффициентами.В общем случае пространственная обработка изображения описывается уравнением: \[G(x,y)=T(I(x,y)),\] где \(G ( x , y )\) - изображение на выходе процедуры обработки; \(I ( x , y )\) - входное изображение для обработки; \(T\) - оператор системы обработки.
Простейшая форма оператора \(T\) достигается, когда окрестность имеет размеры 1 × 1 (один пиксель). В этом случае G зависит только от значения I в точке ( x , y ), и T называется функцией градационного преобразования (функции преобразования интенсивностей или функцией отображения).Градационные методы улучшения изображений.
Рассмотрим некоторые наиболее употребительные градационные методы.Соляризация состоит в том, что участки входного изображения, имеющие уровень белого или близкого к нему уровень яркости, после обработки имеют соответствующий уровень черного. При этом сохраняется уровень черного и участки, имеющие его на оригинальном изображении.
Функция преобразования имеет вид: \(y = k \cdot x \cdot (x_\max-x) \), где \(x_\max \) - максимальное значение выходного сигнала, а k - константа, что позволяет управлять динамическим диапазоном преобразованного изображения. Функция, описывающая данное преобразование, является квадратичной параболой. При \(y_\max = x_\max \) динамические диапазоны изображений совпадают, что может быть достигнуто при \(k = 4 / x_\max. \)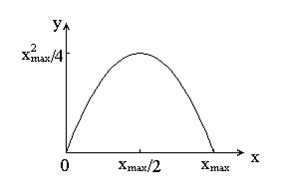 |
| Функция, которая описывает соляризацию. |
 |
| Соляризация изображения Lena. |
Гамма-коррекция яркости.
Наши глаза воспринимают изображения не так, как цифровые устройства. Гамма-коррекция изображений - это процесс, с помощью которого цифровое кодирование изображения приводится в соответствие с нашим восприятием изображения. Этот метод изменения яркости изображения относится к статическим преобразований и описывается выражением: \[ s_{вих}=c\cdot s^\gamma_{вх}, \] где \(с\) и \(\gamma\) - положительные константы, а \(s_{вх}\) и \(s_{вих}\)- соответственно значения яркости на входе и выходе процедуры ее изменения. Вид соответствующих соотношений приведен на картинке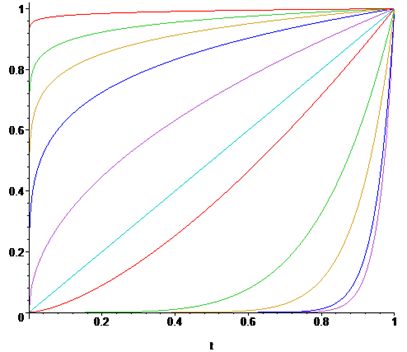 |
| По горизонтали - яркость на входе, по вертикали - на выходе. |
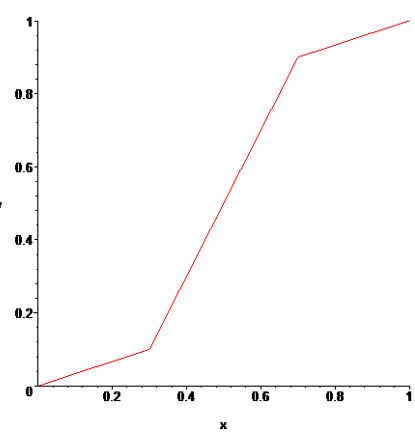 |
| По горизонтали - яркость на входе, по вертикали - на выходе. |
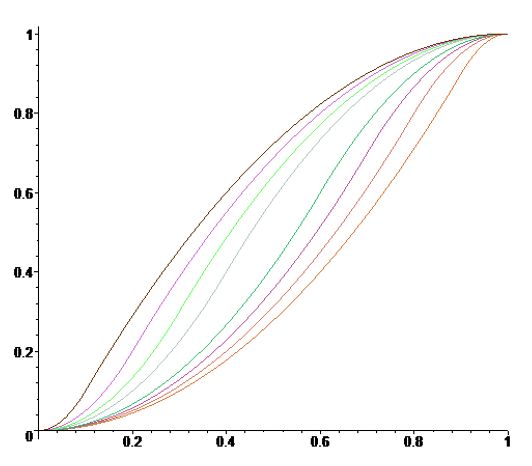
 |
 |

|
| Оригинальное изображение Lena. | Изображение после \(\gamma\)-корекции для \(\gamma=0.5\). | Изображение после сплайн-корекции. |
Гистограммы является исходным материалом для многих методов обработки изображений в пространственной области. Гистограмма является характеристикой количества пикселей в заданном диапазоне освещенности. Поскольку это количество делят на общее количество пикселей, то таким образом, значение нормализованной гистограммы показывают вероятности появления в изображении точек в этом диапазоне освещенности. Очевидно, что сумма вероятностей должна равняться единице.
По виду гистограммы можно сделать некоторые выводы и о самом оригинальном изображении. Например, гистограммы очень темных изображений характеризуются тем, что ненулевые гистограммы сконцентрировано около нулевых уровней яркости, а для очень светлых изображений наоборот - все ненулевые значения сконцентрированы в правой части гистограммы.Рассмотрим методы улучшения изображений путем коррекции их гистограмм.
- Линейная коррекция гистограмм (линейное контрастирование) сводится к изменению диапазона интенсивности входного изображения, так, при наличии области освещения [a, b], надо растянуть его до [0,255], то есть \[\tilde{Y}_{i,j}=255\times \frac{Y_{i,j}-a}{b-a}.\]
- Нормализация гистограммы предполагает не только изменение диапазона интенсивности освещения, но и их наиболее информативные значения. Ясно, что наиболее информативные значения соответствуют пикам гистограмм. Гистограммы, которые соответствуют значениям освещения, встречаются редко, в процессе нормацизации выбрасываются, после чего проводится линейная коррекция.
- Интуитивно можно сделать вывод, что наиболее удобным для восприятия человеком будет изображение, для которого гистограмма близка к равномерному распределению. То есть для улучшения визуального качества, к изображению надо применить такое преобразование, чтобы гистограмма результата содержала все возможные значения яркости и при этом в примерно одинаковом количестве. Такое преобразование называется эквализацией гистограммы.
- Находим гистограмму изображения h.
- Строим функцию распределения за гистограммой \(F(x)=\sum_{i=1}^xh_i\).
- Обновляем пиксели изображения по правилу \[ f(x)=\textrm{round}\left(255×\frac{F(x)-F_\min}{W×H-1}\right). \]
Ниже приведен результат такой процедуры вместе с гистограммами входного и преобразованного изображений.

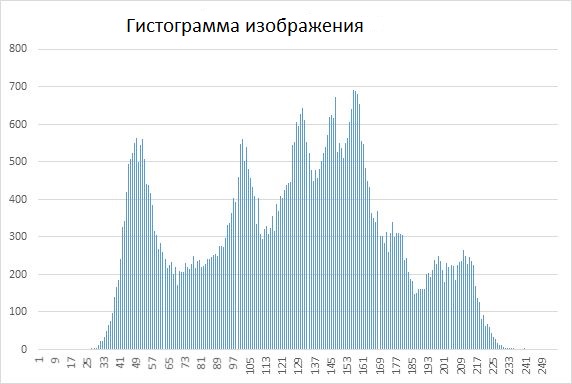

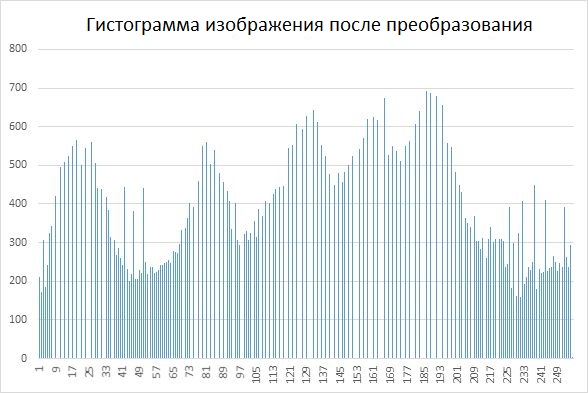
Импульсные шумы и меры уменьшения их влияния.
Медианная фильтрация является эффективным способом подавления импульсных шумов, которые, в частности, неизбежно появляются в цифровых камерах в условиях скудного освещения сцены. Алгоритм медианной фильтрации является масочным:- Для каждой точки входного изображения берется некоторая область (например, ) 3×3
- Точки данной области сортируются по возрастанию яркости.
- Срединная (медианная) точка (5-я для фильтра ) отсортированного множества записывается в итоговое изображение. 3×3
- На следующем шаге окно передвигается на один отсчет и вычисления повторяются. Крайние значения массива дублируются столько раз, чтобы можно было применить окно в первого и до последнего значением.
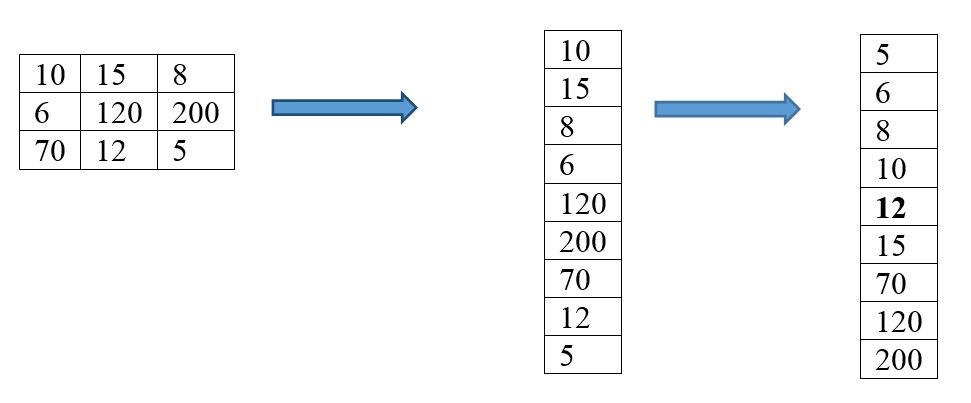 |
| Алгоритм медианной фильтрации. |
Пространственные методы фильтрации с использованием свертки.
Для случая двух переменных свертка непрерывного сигнала \(x(t,\tau)\) с импульсной характеристикой (ядром преобразования) \(h(t,\tau)\) имеет вид \[ y(t,\tau)=h(t,\tau)\otimes x(t,\tau)=\int_{-\infty}^\infty\int_{-\infty}^\infty h(\xi,\eta)x(\xi-t,\eta-\tau)d\xi d\eta. \] Рассмотрим понятие свертки для случая дискретных сигналов. Пусть имеем сигнал \(X\{x_{i,j}\}\) и ядро (маску) преобразования (импульсная характеристика) представляет собой матрицу размером \((N+1)\times (N+1)\), то есть \(H=\{h_{i,j}\}_{i,j=-N}^N\), тогда сверткой \(X\otimes H\) будем называть матрицу \(Y=\{y_{i,j}\}\), такую, что \[ y_{i,j}=\sum_{\nu,\mu=-N}^Nh_{\nu,\mu}x_{i+\nu,j+\mu}. \] Пространственная фильтрация изображений состоит из следующих действий:- Определение центральной точки (x, y) окрестности;
- Осуществление операции, которая использует только значения пикселей с заранее оговоренной области вокруг центральной точки;
- Назначение результата этой операции центральной точке;
- Повторение всего процесса для каждой точки изображения. В результате перемещения позиции центральной точки образуются новые области, соответствующие каждому пикселю изображения.
Линейная фильтрация изображений в пространственной области заключается в вычислении линейной комбинации значений яркости пикселей в окне фильтрации с коэффициентами матрицы весов, называемой маской или ядром линейного фильтра.
Самым простым видом линейной оконной фильтрации в пространственной области является скользящее окно средних значений. Результатом такой фильтрации является значение математического ожидания, вычисленное по всем пикселям окна. Математически это эквивалентно свертке с ядром, все элементы которой равны 1 / n , где n - число элементов ядра, то есть для случая ядра размером имеет вид: \[ \frac{1}{9} \left( \begin{array}{ccc} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \\ \end{array} \right). \] |  |
| Оригинальное изображение Cougar. | Сглаженное изображения Cougar. |
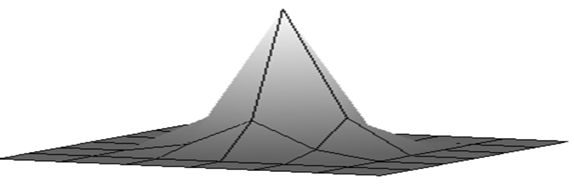
Рассмотрим одну простую конструкцию сглаживания. Будем считать, что данные о поверхности заданные значениями \(z_{i,j}\) в узлах решетки (ih, jh) односвязной области D.
Для построения алгоритмов сглаживания, вместе с каждым значением \(z_{i,j}\), лежащий в середине области D, нужны соседние значения \(z_{i-1,j-1}, z_{i-1,j}, z_{i,j-1}, z_{i+1,j-1}, z_{i-1,j+1}, z_{i+1,j+1}, z_{i+1,j}, z_{i,j+1}\), то есть объект поверхности, соответствующие r-окрестности (\(\sqrt{2}h\le r\le 2h\)) точки (ih,jh).
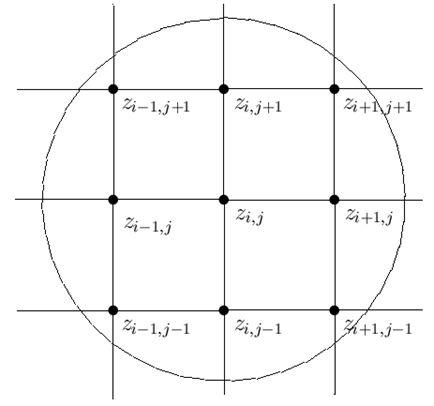
Пусть \(P(x,y)=ax^2+by^2+cxy+dx+ey+f\) квадратичная функция двух переменных. Выберем коэффициенты a, b, c, d, e и f квадратичной функции из условия минимизации суммы квадратов погрешностей, то есть из условия минимума величины \[ \sum_{\nu=i-1}^{i+1}\sum_{\mu=j-1}^{j+1}(z_{\nu,\mu}-P(\nu h,\mu h))^2. \] В качестве сглаженного значения, будем брать значение экстремальной квадратичной функции в точке (ih, jh). Для квадратичной функции необходимые условия минимума совпадают с достаточными. Для определения коэффициентов экстремальной функции необходимо и достаточно взять частные производные от (P (x, y) и приравнять их к нулю. При этом получим систему шести линейных уравнений с шестью неизвестными. Решая ее, получаем квадратичную функцию \[ P^*(x,y)=a^*(x-ih)^2+b^*(y-jh)^2+c^*(x-ih)(y-jh)+d^*(x-ih)+e^*(y-jh)+f^*, \] где \[ a^*=\frac{1}{6h^2}(z_{i-1,j-1}+ z_{i-1,j}+z_{i-1,j+1}+z_{i+1,j-1}+z_{i+1,j}+z_{i+1,j+1}-2(z_{i,j-1}+z_{i,j}+z_{i,j+1})), \] \[ b^*=\frac{1}{6h^2}(z_{i-1,j-1}+ z_{i,j+1}+z_{i-1,j+1}+z_{i+1,j-1}+z_{i,j-1}+z_{i+1,j+1}-2(z_{i-1,j}+z_{i,j}+z_{i+1,j})), \] \[ c^*=\frac{1}{6h^2}(z_{i-1,j-1}+z_{i+1,j+1}-z_{i-1,j+1}-z_{i+1,j-1}), \] \[ d^*=\frac{1}{6h^2}(z_{i+1,j+1}+z_{i+1,j}+z_{i+1,j-1}-z_{i-1,j+1}-z_{i-1,j}-z_{i-1,j-1}), \] \[ e^*=\frac{1}{6h^2}(z_{i+1,j+1}+z_{i-1,j+1}+z_{i,j+1}-z_{i-1,j+1}-z_{i,j-1}-z_{i-1,j-1}), \] \[ f^*=z_{i,j}+\frac{2}{9}(z_{i-1,j}+z_{i,j+1}+z_{i+1,j}+z_{i,j-1}-4z_{i,j}) -\frac{1}{9}(z_{i-1,j+1}+z_{i+1,j+1}+z_{i+1,j-1}+z_{i-1,j-1}-4z_{i,j})= z_{i,j}+\frac{1}{9}(2\Delta^2z_{i,j}-\tilde{\Delta}^2z_{i,j}). \] Таким образом, сглаженным значением можно считать значение \(\tilde{z}_{i,j}\) определяемое равенством \[ \tilde{z}_{i,j}=z_{i,j}+\frac{1}{9}(2\Delta^2z_{i,j}-\tilde{\Delta}^2z_{i,j}), \] где \(\Delta^2z_{i,j}=z_{i-1,j}+z_{i,j+1}+z_{i+1,j}+z_{i,j-1}-4z_{i,j}\) и \(\tilde{\Delta}^2z_{i,j}=z_{i-1,j+1}+z_{i+1,j+1}+z_{i+1,j-1}+z_{i-1,j-1}-4z_{i,j}\).
В этом случае оператор сглаживания порожденный фильтром \[ \frac{1}{9} \left( \begin{array}{ccc} -1 & 2 & -1 \\ 2 & 5 & 2 \\ -1 & 2 & -1 \\ \end{array} \right). \]
Методы изменения резкости изображений.
Ранее были рассмотрены методы пространственной фильтрации, которые приводили к сглаживания изображений. Теперь рассмотрим обратную задачу - повысить контрастность, резкость изображения.Методы, используемые вторые дискретные разницы.
Резкость изображения (его контраст) характеризуется степенью заметности (различение) перепадов яркости соседних участков изображения и если уменьшение резкости (сглаживание) достигается путем применения низкочастотных фильтров, то обратная процедура - повышение резкости связана с использованием высокочастотных фильтров.Визуально повышение резкости приводит к подчеркивание мелких деталей и контуров изображения или улучшение различия тех его деталей, оказались расфокусированным по какой причине.
В дальнейшем нам понадобится первая дискретная разница - аналог первой производной: \[ \frac{\partial s}{\partial x}\to \Delta s[x+1]=s[x+1]-s[x], \] и вторая дискретная разница - аналог второй производной: \[ \frac{\partial^2 s}{\partial x^2}\to \Delta^2 s[x+1]=\Delta s[x+1]-\Delta s[x]=s[x+1]-2s[x]+s[x-1], \] которые широко применяются в методах усиления резкости изображений. В частности, на их использовании основан оператор Лапласа (лапласиан), который для функции двух переменных для аналоговых сигналов определяется как \[ \nabla^2s=\frac{\partial^2 s}{\partial x^2}+\frac{\partial^2 s}{\partial y^2}. \] В простейших случае лапласиан дает ядро свертки \[ \left( \begin{array}{ccc} 0 & -1 & 0 \\ -1 & 4 & -1 \\ 0 & -1 & 0 \\ \end{array} \right) \] но для повышения резкости лучше использовать ядро \[ \left( \begin{array}{ccc} -1 & -1 & -1 \\ -1 & 9 & -1 \\ -1 & -1 & -1 \\ \end{array} \right) \] или ядро 5×5 \[ \left( \begin{array}{ccccc} -1 & -3 & -4 & -3 & -1 \\ -3 & 0 & 6 & 0 & -3 \\ -4 & 6 & 20 & 6 & -4 \\ -3 & 0 & 6 & 0 & -3 \\ -1 & -3 & -4 & -3 & -1 \\ \end{array} \right). \] В целом алгоритм использования лапласиан для повышения резкости изображения имеет вид: \[ \bar{s}[x,y]= \left\{ \begin{array}{lll} s[x,y]-\nabla^2s[x,y]/k, & \hbox{ якщо } & w[0,0]\le 0, \\ s[x,y]+\nabla^2s[x,y]/k, & \hbox{ якщо } & w[0,0]\gt 0. \\ \end{array} \right. \] Результат обработки изображения с применением оператора Лапласу, здесь \(w[0,0]\) - значение центрального коэффициента маски лапласиан. |  |
| Оригинальное изображение Cougar. | Результат применения Лапласиана. |
Градиентные методы.
Кроме аналогов вторых производных, каков лапласиан (оператор Лапласа), для повышения резкости изображения могут быть использованы и операторы первого порядка или градиентные операторы. К ним относятся операторы Робертса, Канне, Собеля и Превити. Они предназначены, в основном, для выделения контуров. Эта процедура является предварительной, кроме повышения резкости изображения, и в других задачах обработки, в частности, задачи распознавания объектов.Принцип работы градиентных операторов удобно рассмотреть на примере алгоритма Собеля. Оператор вычисляет градиент яркости изображения в каждой точке. Так находится направление наибольшего увеличения яркости и величина ее изменения в этом направлении. Результат показывает, насколько резко или плавно меняется яркость изображения в каждой точке, а значит, вероятность нахождения точки на границе и ориентацию границы.
Градиент функции двух переменных для каждой точки изображения (в том числе и функции яркости) - двумерный вектор, компонентами которого являются производные яркости изображения по горизонтали и вертикали. В каждой точке изображения вектор ориентирован в направлении наибольшей изменения яркости, а его длина соответствует величине изменения яркости. Оператор использует ядро 3×3 и с ним сворачивается исходное изображение. Пусть А - входное изображение, а Gx и Gy - две матрицы такого же размера как и изображение, каждая точка которых - производные по x и y \[ Gx=\left( \begin{array}{ccc} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0& 1 \\ \end{array} \right)\otimes A, Gy=\left( \begin{array}{ccc} -1 & -2 & -1 \\ 0 &0 & 0 \\ 1 & 2 & 1 \\ \end{array} \right)\otimes A, \] |  |  |
| Оригинальное изображение Cougar. | Карта сменности освещения по горизонтали. | Карта сменности освещения по вертикали. |
 |
 |
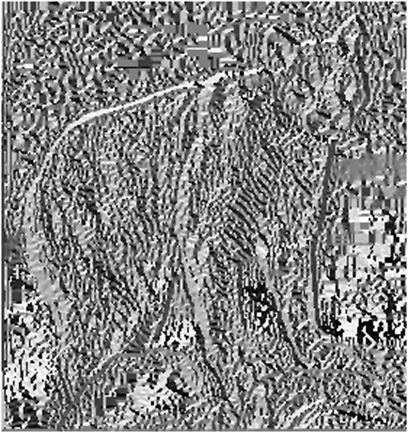
|
| Оригинальное изображение Cougar. | Инверсное изображение величини градиента Cougar. | Карта нормированного направления градиента Cougar. |
Нерезкое маскирование.
Нерезкое маскирование - технологический прием обработки изображения, который позволяет добиться эффекта увеличения резкости за счет усиления контраста тональных переходов. В ходе процедуры происходит объединение немного расплывчатой (нерезкой) версии изображения с оригиналом. В результате получаются резкие детали в высоко контрастных областях без усиления тоновых прыжков в областях с низкой контрастностью там, где резкие тону скачки могут нарушить плавность переходов.Фильтрация с подъемом высоких частот является обобщением процедуры нерезкого маскирования. Эта операция сводится к применению правила контрастирования вида \[ h(x, y)= k\cdot f (x, y) -\nabla^2f (x, y), \] при условии, что весовой коэффициент в центре фильтра меньше нуля, иначе знак перед лапласиан меняется на противоположный. В такой ситуации повышение резкости изображения может проводиться с применением фильтров \[ \left( \begin{array}{ccc} 0 & -1 & 0 \\ -1 &4+k & -1 \\ 0 & -1 & 0 \\ \end{array} \right) \hbox{ або } \left( \begin{array}{ccc} -1 & -1 & -1 \\ -1 &8+k & -1 \\ -1 & -1 & -1 \\ \end{array} \right). \]
 |
 |

|
| Оригинальное изображение Cougar. | Применение нерезкого маскирования с маской М1. | Применение нерезкого маскирования с маской М2.. |
Построение методов восстановления.
Конечно, использование любого метода фильтрации влечет за собой и обратную операцию - восстановление изображения к оригинальному виду, так операция сглаживания порождает операцию контрастности и наоборот. Далее нам понадобится одно утверждение.Через \(\ell^2_2\) обозначим линейное пространство всех ограниченных двумерных последовательностей (массивов) \(A=\{a_{i,j}\}_{(i,j)\in Z^2}\) с нормой \(\|A\|=\left(\sum_{i,j\in Z}a^2_{i,j}\right)^{1/2}\) и положим \(|A|=\left|\sum_{i,j\in Z}a_{i,j}\right|\). Пусть L линейный оператор, который отражает пространство X в пространство Y . Традиционно, нормой оператора L будем называть величину \[ \|L\|_{X\to Y}=\sup \frac{\|L(F)\|_Y}{\|F\|_X\le 1}. \] Обозначим через \(C=A\otimes B\) свертку массивов (матриц) A и B, то есть массив C такой, что \[ c_{i,j}=\sum_{\nu,\mu}a_{\nu,\mu}b_{\nu-i,\mu-j}. \] Рассмотрим уравнение \(E\otimes X=F\), где |E|≠ 0, тогда \(\frac{E}{|E|}\otimes X=\frac{F}{|E|}\), или, что то же, \(\tilde{E}\otimes X=\Phi\), где \(\tilde{E}=\frac{E}{|E|}\) и \(\Phi = \frac{F}{|E|}\).
Основой для построения восстановительных фильтров является следующее утверждение:
Теорема. Если для любого натурального n выполняется неравенство то имеет место соотношение \begin{equation}\label{1} \|I-\tilde{E}\|_{\ell^2_2\to\ell^2_2}\lt 1, \end{equation} тогда имеет место соотношение \begin{equation}\label{2} X_n=C^1_n\Phi-C^2_n\tilde{E}\otimes \Phi+C^3_n\tilde{E}^2\otimes \Phi+...+(-1)^nC^n_n\tilde{E}^n\otimes \Phi+\varepsilon_n \end{equation} где \(\varepsilon_n\) такое, что \begin{equation}\label{3} \tilde{E}\otimes \varepsilon_n=\left(I-\tilde{E}\right)^{n+1}\otimes \Phi. \end{equation} Действительно, если \[ X_n=C^1_n\Phi-C^2_n\tilde{E}\otimes \Phi+C^3_n\tilde{E}^2\otimes \Phi+...+(-1)^nC^n_n\tilde{E}^n\otimes \Phi+\varepsilon_n \] то \[ \tilde{E}\otimes X_n=\tilde{E}\otimes\left(C^1_n\Phi-C^2_n\tilde{E}\otimes \Phi+C^3_n\tilde{E}^2\otimes \Phi+...+(-1)^nC^n_n\tilde{E}^n\otimes \Phi+\varepsilon_n\right)= \tilde{E}\otimes C^1_n\Phi-C^2_n\tilde{E}^2\otimes \Phi+C^3_n\tilde{E}^3\otimes \Phi+...+(-1)^nC^n_n\tilde{E}^{n+1}\otimes \Phi+ \tilde{E}\otimes \varepsilon_n. \] Отсюда и из (\ref{3}) сразу получаем \[ \tilde{E}\otimes X_n=\tilde{E}\otimes C^1_n\Phi-C^2_n\tilde{E}^2\otimes \Phi+C^3_n\tilde{E}^3\otimes \Phi+...+(-1)^nC^n_n\tilde{E}^{n+1}\otimes \Phi+ \left(I-\tilde{E}\right)^{n+1}\otimes \Phi= \] \[ \tilde{E}\otimes C^1_n\Phi-C^2_n\tilde{E}^2\otimes \Phi+C^3_n\tilde{E}^3\otimes \Phi+...+(-1)^nC^n_n\tilde{E}^{n+1}\otimes \Phi+ \Phi-\tilde{E}\otimes C^1_n\Phi+C^2_n\tilde{E}^2\otimes \Phi-C^3_n\tilde{E}^3\otimes \Phi+...+(-1)^{n+1}C^n_n\tilde{E}^{n+1}\otimes \Phi=\Phi. \] Отметим, что, если выполняется условие (\ref{1}), то \[ \|\varepsilon_n\|\le |\tilde{E}^{-1}|\|I-\tilde{E}\|^{n+1}|\Phi|, \] и в этом случае, решение можно записать в операторной виде \[ X=\lim_{n\to \infty}\left(I-\left(I-\tilde{E}\right)^n\right)\Phi. \] Используем этот результат для построения оператора контрастности, что возвращает изображения, изменено в результате применения оператора сглаживания.В качестве примера рассмотрим построение контрастирующего фильтра псевдообратного к сглаживающему фильтру S, построенного ранее: \[ S=[s_{i,j}]_{i,j=-1}^1=\frac{1}{9}\left( \begin{array}{ccc} -1 & 2 & -1 \\ 2 &5 & 2 \\ -1 & 2 & -1 \\ \end{array} \right). \]
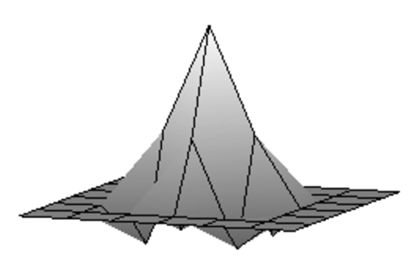
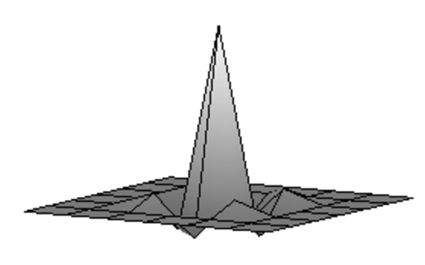
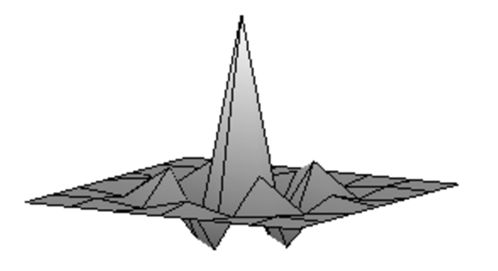
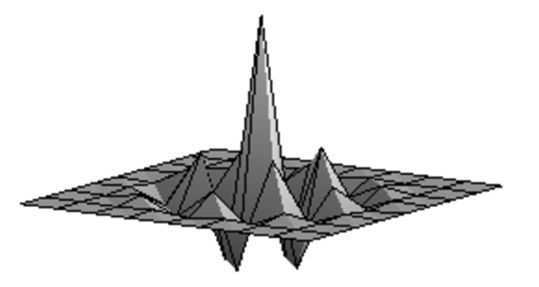

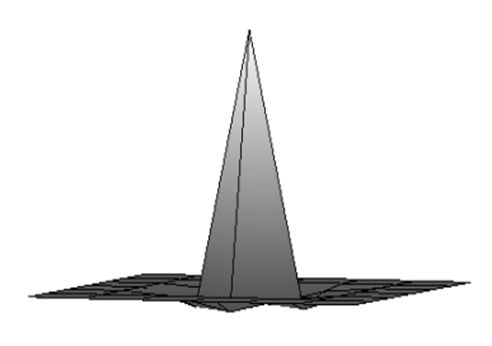
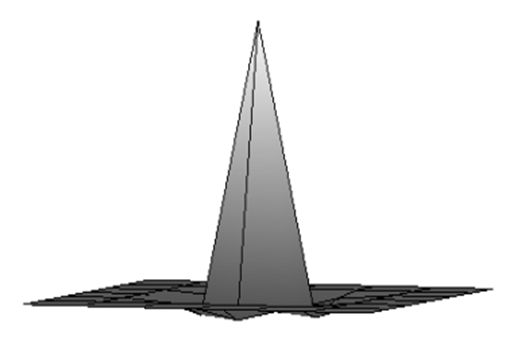

| Сглаженое изображение. | Результат после применения обратного фильтра первой итерации. |
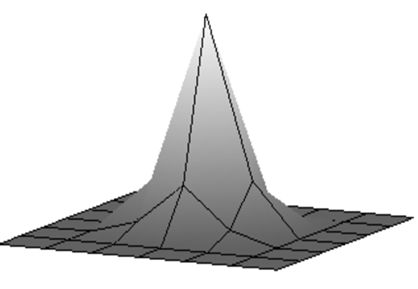
Результат после применения обратного фильтра второй итерации. |
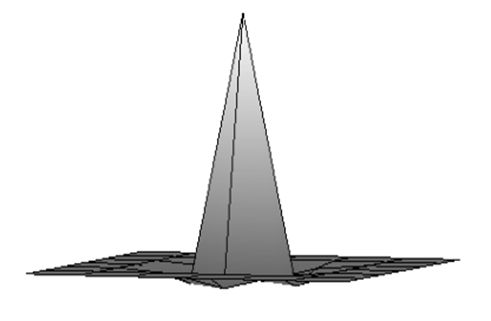
Результат после применения обратного фильтра третьей итерации. |
 |
 |

|
 |
| PSNR=27.26. | PSNR=32.08. | PSNR=35.53. | PSNR=37.96. |
PSNR чаще всего используется для измерения качества реконструкции изображений. Сигнал в этом случае являются исходными данными, а шум - это ошибка.
Типичные значения PSNR для сравнения изображений лежат в пределах от 30 до 40 dB. Чем выше значение PSNR, тем меньше разница между изображениями, сравниваются.Для монохромных изображений I и K размера H×W, одно из которых является зашумленным приближением другого, PSNR вычисляется следующим образом \[ PSNR=20\times \rm{lg} \frac{\max \{I\}}{\sqrt{MSE}}, \] где \[ MSE=\frac{1}{H\times W}\sum_{i=1}^W\sum_{j=1}^H|I_{i,j}-K_{i,j}|^2. \] В случае сравнения полноцветовых изображений, используем сумму MSE по каждй цветовой компоненте и поделим на 3.
В завершение параграфа, посвященного созданию пространственных фильтров, рассмотрим реализацию эффекта акварелизации. Акварельный фильтр преобразует изображение, и, после обработки оно выглядит так, как будто написано акварелью. Для получения такого эффекта используется метод медианного усреднения цвета в каждой точке. Значение цвета каждого пиксела и его 24 соседей помещаются в список и сортируются от меньшего к большему. Медианное (тринадцатая) значение цвета в списке присваивается центральном пикселу. После этого, для выделения границы переходов цветов, к полученному изображению применяется контрастирующий фильтр. Результирующее изображение напоминает акварельную живопись.


Морфологическая обработка бинарных изображений.
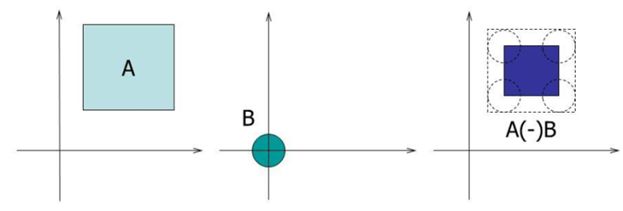
Расширение (Dilation) \[ A\ominus B=(A^c\oplus B^c)^c, \] где \(А^с\) дополнение А.
 |
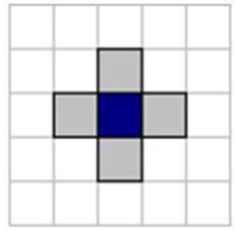 |
| A | B |
 |
 |

|
 |
| \(А\oplus В\) Расширение (dilation) |
\(А\ominus В\) Сужение (erosion) |
\((А\oplus В)\ominus В\) Открытие (open) |
\((А\ominus В) \oplus В\) Закрытие (close) |
 |
| Костел святого Николая (м.Каменское) конец ХІХ в. |
 |
 |
| A | B |
 |
 |
| \(А\oplus В\) Расширение (dilation) |
\(А\ominus В\) Сужение (erosion) |
 |
 |
| \((А\oplus В)\ominus В\) Открытие (open) |
\((А\ominus В) \oplus В\) Закрытие (close) |
Использование морфологической обработки для находжения контура.
Формирование внутреннего контура \( C^-=A-(A\ominus B) \)


 |
 |
| \(А\oplus В\) Расширение (dilation) |
\(А\ominus В\) Сужение (erosion) |
 |
 |
| \((А\oplus В)\ominus В\) Открытие (open) |
\((А\ominus В) \oplus В\) Закрытие (close) |
Цель морфологической обработки:
- Снижение шумов.
- Выделение границ объекта.
- Выделение скелета объекта.
- Модификация контурного представления.
Сегментация изображений.
Сегментация разделяет изображение на отдельные регионы, содержащих пиксели с подобными значениями. Для того, чтобы быть полезными для анализа и интерпретации изображений, регионы должны сильно связываться с изображенными объектами или интересными (для пользователя) признакам. Технологии сегментации могут быть либо контекстными или неконтекстное. Последние не учитывают пространственных связей между функциями изображения и группировки пикселей вместе на основе некоторого глобального атрибута, например, одного уровня или цвета. Контекстные методы дополнительно используют эти связи, например, объединяют пиксели с подобными уровнями и близким пространственным расположением.k-means
Данный метод сегментации является неконтекстным и изображение сегментируется по близости цветов RGB. Мерой близости есть евклидово расстояние.В основе данного подхода лежит метод кластеризации k-средними (k-means) (см., например, здесь).
Идея метода k-средних заключается в следующем - сначала выбирается k произвольных начальных центров из множества \(\mathfrak{T}\). Далее все объекты разбиваются на k групп, наиболее близких к соответствующему центра. На следующем шаге вычисляются центры найденных кластеров. Процедура повторяется итерационно до тех пор, пока центры кластеров не стабилизируются.Алгоритм разбиения объектов \(x_i (i=0,1,…,n)\) основан на минимизации межкластерного расстояния, в случае, если в качестве расстояния используется середньеквадратическая норма \(\ell_2\), то есть целевой функцией есть \[ J=\sum_{j=1}^k\sum\left\{\left.\|x_i-\mu_j\|^2\right|x_i\in C_j\right\}, \] где \(x_i\)-i -й объект, а \(C_j\) представляет собой j -й кластер с центром \(\mu_j\).
Структура алгоритма заключается в следующем:
- Для инициализации алгоритма выбираем k центров кластеров.
- Каждому из n объектов поставим в соответствие кластер, исходя из минимизации \(\ell_2\) нормы между объектом и центром соответствующего кластера.
-
Пересчитаем центры вновь полученных кластеров.
Для решения этой задачи среди всех элементов кластера \(x\in C_j\) найдем элемент \(\mu_j\), который минимизирует отклонение \(\sum\left\{\left.\|x_i-\mu_j\|^2\right|x_i\in C_j\right\}\), для чего найдем решение задачи \[ \frac{\partial}{\partial\mu_j}\sum_{x_i\in C_j}\|x_i-\mu_j\|^2=-2\sum_{x_i\in C_j}(x_i-\mu_j)=0, \] то есть \[ \mu_j=\frac{1}{n_j}\sum_{x_i\in C_j}x_i. \] - Для каждого \(i\) , такого, что \(x_i\in C_j\) найдем \[ h=\rm{argmin}\left\{\frac{n_j \|x_i-\mu_j\|}{n_j-1}\right\}, \] где \(n_j\) число объектов кластера \(C_j\).
- Если выполняется условие \[ \frac{n_h\|x_i-\mu_h\|}{n_h-1}\lt \frac{n_j\|x_i-\mu_j\|}{n_j-1}, \] тогда следует переместить объект \(x_i\) из кластера \(C_j\) в кластер \(C_h\), после чого пересчитать значения центров кластеров.
- Если \(i\lt n\), то переходим к шагу 4, иначе к шагу 3.
В нашем случае для двух пикселей \(X(X_{red},X_{green}, X_{blue} )\) и \(Y(Y_{red},Y_{green}, Y_{blue} )\) расстояние между ними равно \[ \|X-Y\|^2=(X_{red}-Y_{red})^2+(X_{green}-Y_{green})^2+(X_{blue}-Y_{blue})^2 \] и цвет пикселей всего кластера \(C_j\) совпадает с цветом центра кластера \(\mu_j\).
Для тестового изображения Lena в случае k=8 получаем

EM-алгоритм.
В основе данного неконтекстного метода сегментации лежит анализ смеси распределений \[ p(x)=\sum_{i=1}^k\omega_ip_i(x). \] в предположении, что известен только общий вид распределения вероятности и нужно оценить его параметры.Для решения этой задачи используется EM-алгоритм (см., например, здесь ). EM-алгоритм для известного фиксированного числа компонентов смеси можно записать в следующем виде.
Пусть \(X=\{x_1,…,x_n \}\) выборка наблюдений, k число компонентов смеси, \(\Theta=\{(w_i,\theta_i )\}_{i=1}^k\)- начальное приближение параметров смеси, и ε число, определяющее остановку алгоритма.EM-алгоритм состоит из последовательного применения двух шагов.
Е-шаг (expectation) \[ g_{i,j}^0=g_{i,j}, \] \[ g_{i,j}=\frac{\omega_ip_i(x_j)}{\sum_{\nu=1}^k\omega_\nu p_\nu(x_j)},i=1,…,k,j=1,…,n. \] \[ \delta=\max\{|g_{i,j}^0-g_{i,j} |\}. \] M-шаг (maximization) \[\sum_{j=1}^ng_{i,j}\rm{ln } p_i(x_j)\to \max_\Theta,i=1,…,k, \] \[ w_i=\frac{1}{n}\sum_{j=1}^ng_{i,j} ,i=1,…,k. \] Если δ>ε, то переходим к Е-шагу, если δ≤ ε, то возвращаем найденные параметры смеси, \(\Theta=\{(w_i,\theta_i )\}_{i=1}^k\).В случае смеси нормальных распределений \(N(\mu_i,\sigma_i^2)\) Е-шаг будет выглядеть следующим образом \[ g_{i,j}=\frac{\omega_ip_i(x_j)}{\sum_{\nu=1}^k\omega_\nu p_\nu(x_j)},i=1,…,k,j=1,…,n. \] где \[ p(x|\mu_i,\sigma_i)=\frac{1}{\sigma_i\sqrt{2\pi}}\exp\left(-\frac{(x-\mu_i)^2}{2\sigma_i^2}\right). \] Для М-шага задача \[ \sum_{j=1}^ng_{i,j}\ln p_i(x_j)\to \max_{\Theta}, i=1,...,k, \] запишется в следующем виде \[ \sum_{j=1}^ng_{i,j}\ln \left(\frac{1}{\sigma_i\sqrt{2\pi}}\exp\left(-\frac{(x-\mu_i)^2}{2\sigma_i^2}\right)\right)\to \max_{\Theta}, i=1,...,k, \] или, что тоже \[ G\left(\left\{\mu_i,\sigma_i\right\}_{i=1}^k\right)=\sum_{j=1}^ng_{i,j} \left(-\ln\left(\sigma_i\sqrt{2\pi}\right)-\frac{(x-\mu_i)^2}{2\sigma_i^2}\right)\to \max_{\Theta}, i=1,...,k. \] Найдем производные и приравняем их к нулю \[ \frac{\partial}{\partial \mu_i}G\left(\left\{\mu_i,\sigma_i\right\}_{i=1}^k\right)=-\sum_{j=1}^ng_{i,j}\frac{x-\mu_i}{\sigma_i^2}=0, \] отсюда \[ \mu_i=\frac{\sum_{j=1}^ng_{i,j}x_j}{\sum_{j=1}^ng_{i,j}}. \] Аналогично, \[ \frac{\partial}{\partial \sigma_i}G\left(\left\{\mu_i,\sigma_i\right\}_{i=1}^k\right)= -\sum_{j=1}^ng_{i,j} \left(\frac{1}{\sigma_i}-\frac{(x-\mu_i)^2}{\sigma_i^3}\right)= -\sum_{j=1}^ng_{i,j} \left(\frac{\sigma_i^2-(x-\mu_i)^2}{\sigma_i^3}\right)=0, \] таким образом, \[ \sigma_i^2=\frac{\sum_{j=1}^ng_{i,j}(x-\mu_i)^2}{\sum_{j=1}^ng_{i,j}}, \] что позволяет получить параметры в явном виде.
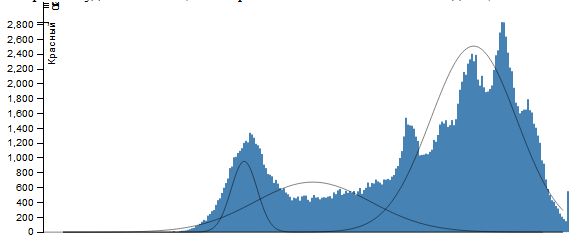
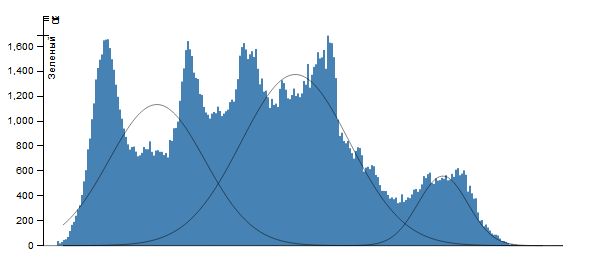
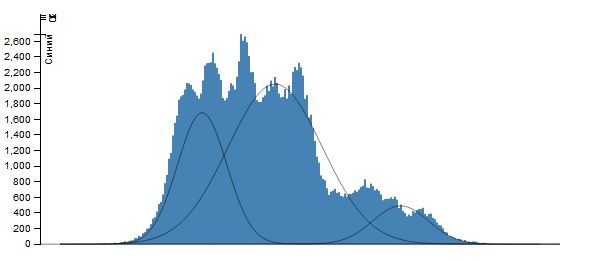
Применение ЭМ-алгоритма к сегментации изображений.
Для этой цели построим гистограмму цвета для каждой компоненты - красного, зеленого и синего. По оси x меняется интенсивность цвета от 0 до 255, а по оси y - количество пикселей с данной интенсивностью.Считая, что каждая гистограмма представляет собой смесь функций Гаусса \[ \sum_{i=1}^n\frac{\omega_i}{\sigma_i\sqrt{2\pi}}\exp\left(-\frac{(x-\mu_i)^2}{2\sigma_i^2}\right) \] применим EM-алгоритм с заданным количеством элементов смеси n (это же количество сегментов, на которое мы разбиваем каждую цветовую плоскость изображения). И как результат, пусть множество значений интенсивности \(X_j=(x_j,x_{j+v_j }\) ) таково, что \[ \forall x\in X_j: \frac{\omega_j}{\sigma_j\sqrt{2\pi}}\exp\left(-\frac{(x-\mu_j)^2}{2\sigma_j^2}\right)\ge \frac{\omega_i}{\sigma_i\sqrt{2\pi}}\exp\left(-\frac{(x-\mu_i)^2}{2\sigma_i^2}\right) (i\ne j). \] Тогда всем точкам, интенсивность которых лежит в промежутке \(X_j\), поставим в соответствие значение \(\mu_j\) (при практической реализации - ее целую часть). Результатом работы алгоритма будет сегментация изображения на n сегментов по каждой цветовой компоненте.
Для изображения Lena при \(k=3\) имеем

EM-алгоритм для случая двух переменных.
Данный метод можно обобщить на случай двух переменных и сделать контентным, то есть рассмотреть зависимость пикселей не только по цвету, но и по их положением - по координатам (x, y). Как видно из рассмотренного ЭМ-алгоритма, при использовании данных двух переменных (i,j,r_(i,j) ), (i,j,g_(i,j) ), (i,j,b_(i,j) ) каждую из множеств можно описать линейной комбинацией двумерных функций Гаусса \[ \frac{1}{2\pi|\Sigma_i^{-1}|^{1/2}}\exp\left(-\frac{1}{2}(x-\mu_i)^T\Sigma_i^{-1}(x-\mu_i)\right) \] с помощью ЭМ-алгоритма аналогично тому, как было сделано в одномерном случае.Отметим, что для двумерного случая нормальное распределение определяется следующим образом \[ p\left(x|\mu_i,\Sigma_i\right)=\frac{1}{2\pi|\Sigma_i^{-1}|^{1/2}}\exp\left(-\frac{1}{2}(x-\mu_i)^T\Sigma_i^{-1}(x-\mu_i)\right) \] где \(\Sigma_i\)-кореляционная матрица и параметры равны \[ \mu_i=\frac{\sum_{j=1}^ng_{i,j}x_j}{\sum_{j=1}^ng_{i,j}} \] и \[ \Sigma_i=\frac{\sum_{j=1}^ng_{i,j}(x_j-\mu_i)(x_j-\mu_i)^T}{\sum_{j=1}^ng_{i,j}}. \]
Пороговая и мультипороговая сегментация.
Пороговая сегментация изображения по уровням яркости - самый простой вид сегментации изображения. Этот метод основан на том, что многие объекты или области изображения характеризуются постоянной отражательной способностью или поглощением света на их поверхности. Отличительной чертой пороговой сегментации является вычислительная эффективность и возможность использования в системах реального масштаба времени.Пороговая сегментация выполняется следующим образом: \[ Bin_{i,j}= \left\{ \begin{array}{ll} 1, & \hbox{якщо }I_{i,j}\ge T,\\ 0, & \hbox{якщо }I_{i,j}\lt T, \end{array} \right. \] где \(Bin_{i,j}\) - элемент результирующего бинарного изображения, \(I_{i,j}\)- элемент исходного изображения.
Успех пороговой сегментации зависит от способа выбора порога \(T\). При использовании метода Оцу, изображение разбивается на передней и на задней план, то есть, проводится бинаризации изображения.Мультипороговая сегментация.
Используется в том случае, если исходное изображение характеризуется не бимодальной, а мультимодальной гистограммой. В этом случае результирующее изображение разбивается на несколько уровней: \[ G_{i,j}= \left\{ \begin{array}{ll} 1, & \hbox{ если }I_{i,j}\in D_1,\\ 2, & \hbox{ если }I_{i,j}\in D_2,\\ ...\\ n, & \hbox{ если }I_{i,j}\in D_n,\\ 0, & \hbox{ иначе }. \end{array} \right. \] Рассмотрим задачу выбора порогов при мультипороговой сегментации. По сути, решение этой задачи сводится к построению гистограммы с заданным числом узлов n<255 ,которая наилучшим образом аппроксимирует гистограмму изображения. Распределение узлов этой гистограммы с малым числом узлов и является распределением порогов.О построении асимптотически оптимальных гистограмм.
Термин гистограмма ввел Карл Пирсон еще в 1895 году. Гистограммы позволяют увидеть, как распределены значения переменных по интервалам группировки, насколько сильно они различаются между собой, как сконцентрировано большинство наблюдений вокруг среднего, является распределение симметричным или нет, имеет ли оно одну моду и прочее.Пусть \(X_1,X_2,...,X_N\)-виборка заданного распределения, разбиение \(\Delta_n=\{-\infty\lt x_0\lt x_1\lt ...\lt x_n\lt \infty\}\) с шагом \(h_{i-1/2}=x_i-x_{i-1}\) и \(m_i=\sum_{i=1}^N\left\{1\left|X_k\in (x_{i-1},x_{i}]\right.\right\},i=1,...,n\) число элементов из i -го интервала выборки. Тогда кусочно постоянная функция \(H:R\to R\) \[ H(x)=H(\Delta_n,x)=m_i,x\in (x_{i-1},x_i],i=1,2,...,n \] называется гистограммой выборки \(X_1,X_2,...,X_N\), если же кусочно постоянная функция \(H:R\to R\) такова, что \[ \hat{H}(x)=\hat{H}(\Delta_n,x)=\frac{m_i}{Nh_{i-1/2}},x\in (x_{i-1},x_i],i=1,2,...,n, \] то она называется нормализованной гистограммой. Заметим, что нормализованная гистограмма является функцией плотности вероятности, потому что \[ \hat{H}(t)\ge 0 \hbox{ при } t\in R \hbox{ и, кроме того, }\int_{-\infty}^\infty \hat{H}(t)dt=1. \] Для абсолютно непрерывных распределений случайных величин с плотностью вероятности \(f(x)\)для нормализованных гистограмм при \(N\to\infty\) \[ \forall x\in (x_{i-1},x_i], \hat{H}(x)=\frac{m_i}{Nh_{i-1/2}}\to P\left(X\in (x_{i-1},x_i]\right)\equiv \int_{x_{i-1}}^{x_i}f(x)dx,i=1,2,...,n. \] Таким образом, для непрерывной случайной величины, гистограмма на каждом участке своего постоянного значения должна сохранять среднее значение. Традиционно рассматриваются гистограммы с равноудаленными узлами, но выбор узлов гистограмы существенно влияет на качество описания случайного процесса. Рассмотрим задачу построения гистограммы с асимптотически оптимальными узлами.
Обозначим через \(\Delta_n=\{x_i\}_{i=0}^n\)- произвольное разбиение \(\Delta_n=\{0= x_0\lt x_1\lt ...\lt x_n=T\}\), положим \(h_{i+1/2}=x_{i+1}-x_i\), \(h=\max_ih_{i+1/2}\) и \(x_{i+\frac{1}{2}}=\frac{x_{i}+x_{i+1}}{2}\). Через \(S\left(\left\{a_{i+\frac{1}{2}}\right\}_{i=1}^{n-1},\Delta_n,x\right)\) обозначим кусочно-постоянную функцию со значениями \(a_{i+\frac{1}{2}}\) для \(x\in [x_i,x_{i+1})\).Для функции \(y(x)\) , непрерывной на [0,T], рассмотрим задачу \[ \varepsilon=\min_{x_i}\min_{a_{i+\frac{1}{2}}}\sum_{i=0}^{n-1}\int_{x_i}^{x_{i+1}}\left(a_{i+\frac{1}{2}}-y(x)\right)^2dx. \] Теорема 1. Пусть \(y(x)\) - непрерывно дифференцируемая функция \(y\in C^2_{[0,T]}\) такая, что \(y'(x)\) на промежутке \([0,T]\) имеет не более конечного числа нулей, тогда \[ \varepsilon=\frac{1}{12n^2}\left(\int_0^T\left(y'(x)\right)^{\frac{2}{3}}dx\right)^3+O\left(\frac{1}{n^3}\right) \] и при этом минимум достигается для разбиения \(\Delta^*_n=\{x^*_i\}_{i=0}^n\) такого, что \[ \int_{x^*_i}^{x^*_{i+1}}\left(y'(x)\right)^{\frac{2}{3}}dx=\frac{1}{n}\int_0^T\left(y'(x)\right)^{\frac{2}{3}}dx \hbox{ і } a_{i+\frac{1}{2}}^*=\frac{1}{h^*_{i+\frac{1}{2}}}\int_{x^*_i}^{x^*_{i+1}}y(x)dx. \] Докажем это утверждение. Вначале рассмотрим следующую задачу \[ \Phi\left(a_{i+\frac{1}{2}}\right)=\int_{x_i}^{x_{i+1}}\left(a_{i+\frac{1}{2}}-y(x)\right)^2dx\to\min_{a_{i+\frac{1}{2}}}. \] Тогда учитывая выпуклость задачи, необходимое условие минимума является и достаточным, то есть, решение этой задачи находится из уравнения \[ \frac{d}{da_{i+\frac{1}{2}}}\Phi\left(a_{i+\frac{1}{2}}\right)=2\int_{x_i}^{x_{i+1}}\left(a_{i+\frac{1}{2}}-y(x)\right)dx=0, \] и тогда, \[ a_{i+\frac{1}{2}}=\frac{1}{h_{i+\frac{1}{2}}}\int_{x_i}^{x_{i+1}}y(x)dx. \] Таким образом первоначальную задачу можно переписать в виде \[ \varepsilon=\min_{x_i}\sum_{i=0}^{n-1}\int_{x_i}^{x_{i+1}}\left(y(x)-\frac{1}{h_{i+\frac{1}{2}}}\int_{x_i}^{x_{i+1}}y(x)dx\right)^2dx. \] Испльзуя формулу Тейлора \[ y(x)=y_{i+\frac{1}{2}}+y'_{i+\frac{1}{2}}\left(x-x_{i+\frac{1}{2}}\right)+O(h^2), \] где \(h=\max_ih_{i+\frac{1}{2}}\), получаем \[ \varepsilon=\min_{x_i}\sum_{i=0}^{n-1}\int_{x_i}^{x_{i+1}}\left(y_{i+\frac{1}{2}}+y'_{i+\frac{1}{2}}\left(x-x_{i+\frac{1}{2}}\right)+O(h^2) -\frac{1}{h_{i+\frac{1}{2}}}\int_{x_i}^{x_{i+1}}\left(y_{i+\frac{1}{2}}+y'_{i+\frac{1}{2}}\left(x-x_{i+\frac{1}{2}}\right)+O(h^2)\right)dx\right)^2dx= \] \[ =\min_{x_i}\sum_{i=0}^{n-1}\int_{x_i}^{x_{i+1}}\left(y_{i+\frac{1}{2}}+y'_{i+\frac{1}{2}}\left(x-x_{i+\frac{1}{2}}\right)- y_{i+\frac{1}{2}}+O(h^2)\right)^2dx= \min_{x_i}\frac{1}{12}\sum_{i=0}^{n-1}\left(\left(y'_{i+\frac{1}{2}}\right)^2h^3_{i+\frac{1}{2}}+O(h^4)\right). \] Из теоремы о среднем для интегралов имеем, что найдется точка \(\xi_{i+\frac{1}{2}}\in [x_i,x_{i+1}]\) такая, что \[ \left(y'\left(\xi_{i+\frac{1}{2}}\right)\right)^2h^3_{i+\frac{1}{2}}= \left(\left(y'\left(\xi_{i+\frac{1}{2}}\right)\right)^{\frac{2}{3}}h_{i+\frac{1}{2}}\right)^3= \left(\int_{x_i}^{x_{i+1}}\left(y'(x)\right)^{\frac{2}{3}}dx\right)^3, \] Отсюда и из предыдущего сразу имеем \[ \varepsilon=\min_{x_i}\frac{1}{12}\sum_{i=0}^{n-1}\left(\left(y'_{i+\frac{1}{2}}\right)^2h^3_{i+\frac{1}{2}} +\left(y'\left(\xi_{i+\frac{1}{2}}\right)\right)^2h^3_{i+\frac{1}{2}}- \left(y'\left(\xi_{i+\frac{1}{2}}\right)\right)^2h^3_{i+\frac{1}{2}} +O(h^4)\right)=\min_{x_i}\frac{1}{12}\sum_{i=0}^{n-1}\left(\left( \int_{x_i}^{x_{i+1}}\left(y'(x)\right)^{\frac{2}{3}}dx\right)^3+O(h^4)\right). \] Лемма. Пусть \(\alpha\gt 0\) и \(C\gt 0\), тогда \[ \min\left\{\sum_{i=0}^{n-1}C^\alpha_i|C_i\ge 0,\sum_{i=0}^{n-1}C_i=C\right\}=n\left(\frac{C}{n}\right)^\alpha, \] и при этом минимум достигается тогда, когда все \(C_i \) равны между собой, то есть, \[ C^*_i=\frac{C}{n},i=0,...,n-1. \] Для доказательства этого утверждения используем метод неопреленных множителей Лагранжа.
Выпишем функцию цели \[ \mathfrak{L}=\lambda_0\sum_{i=0}^{n-1}C_i^\alpha+\lambda_1\left(\sum_{i=0}^{n-1}C_i-C\right), \] тогда \[ \frac{\partial\mathfrak{L}}{\partial C_i}=\lambda_0\alpha C_i^{\alpha-1}+\lambda_1=0, \] і \(\lambda_0\alpha(C_i^{\alpha-1}+\lambda_2)=0,\) де \(\lambda_2=\frac{\lambda_1}{\lambda_0\alpha}\).
Таким образом, имеем \(C_i=-\lambda_2^{\frac{1}{\alpha-1}}\) і \[ \sum_{i=0}^{n-1}C_i=-\sum_{i=0}^{n-1}\lambda_2^{\frac{1}{\alpha-1}}=-n\lambda_2^{\frac{1}{\alpha-1}}=C. \] Отсюда \(\lambda_2^{\frac{1}{\alpha-1}}=-\frac{C}{n}\), или, что то же самое, \(C_i=\frac{C}{n}, i=0,...,n-1.\).Лемма доказана.
Таким образом, возвращаясь к доказательству теоремы из доказанной леммы имеем \[ \varepsilon=\min_{x_i}\frac{1}{12}\sum_{i=0}^{n-1}\left(\left( \int_{x_i}^{x_{i+1}}\left(y'(x)\right)^{\frac{2}{3}}dx\right)^3+O(h^4)\right)= \frac{1}{12}\sum_{i=0}^{n-1}\left(\left( \int_{x^*_i}^{x^*_{i+1}}\left(y'(x)\right)^{\frac{2}{3}}dx\right)^3+O(h^4)\right)= \frac{1}{12}\left(\int_0^T\left(y'(x)\right)^{\frac{2}{3}}dx\right)^3+O\left(\frac{1}{n^3}\right) \] и при этом минимум достигается для разбиения \(\Delta^*_n=\{x^*_i\}_{i=0}^n\) такого, что \[ \int_{x^*_i}^{x^*_{i+1}}\left(y'(x)\right)^{\frac{2}{3}}dx=\frac{1}{n}\int_0^T\left(y'(x)\right)^{\frac{2}{3}}dx. \] Кроме того, отметим, что для заданной погрешности \(\varepsilon \) можно найти количество узлов n кусочно-постоянной функции \(S\left(\left\{a_{i+\frac{1}{2}}\right\}_{i=1}^{n-1},\Delta_n,x\right)\) с асимптотически оптимальными узлами, которые выбираются из условия выше \[ n=\left[\sqrt{\frac{1}{12\varepsilon}\left(\int_0^T\left(y'(x)\right)^{\frac{2}{3}}dx\right)^3}\right]+1, \] где \([\cdot]\) - целая часть числа.Идея полученного результата состоит в том, что узлы распределяются таким образом, чтобы погрешности приближения на каждом отрезке функции \(x (t) \) кусочно-постоянной функцией \(S \left (\left \{a_ {i + \frac{1}{2}} \right \}_{i = 1}^{n-1 } \Delta_n, x \right) \) будут равны между собой.
Распределение узлов \(S\left(\left\{a_{i+\frac{1}{2}}\right\}_{i=1}^{n-1},\Delta_n,x\right)\) при приближении гистограммы изображения может служить множеством порогов для сегментации данного изображения.Алгоритм выбора асимптотически оптимальных порогов сегментации.
Опираясь на полученные результаты, формализируем алгоритм выбора порогов сегментации. Пусть \(\{\hbar_i \}_{i=0}^255\) –гистограмма интерсивности освещения (компоненты Y). Найдем \[ d_i=|\hbar_{i+1}-\hbar_i |^{2/3},i=0,…,254. \] Далее \[ φ(0)=0,φ(k)=\sum_{i=0}^kd_i, k=1,…,254. \] В случае известного числа сегментов n пороги \(T_j, j = 0,1, ..., n \) находятся следующим образом \[ T_0=0,\frac{(j-1)\varphi(254)}{n}\le\varphi\le\frac{j\varphi(254)}{n},j=1,…,n. \] Таким образом, можно разбить изображение на сегменты по вычисленным порогам.Ясно, что каждый сегмент будет состоять из нескольких не связанных с собой областей. Следующим шагом будет слияние областей, то есть, если количество точек, из которых состоит область, меньше заданного числа К, то данную область будем объединять с той соседней областью, уровень сегментации которой наиболее схож с уровнем текущей области.
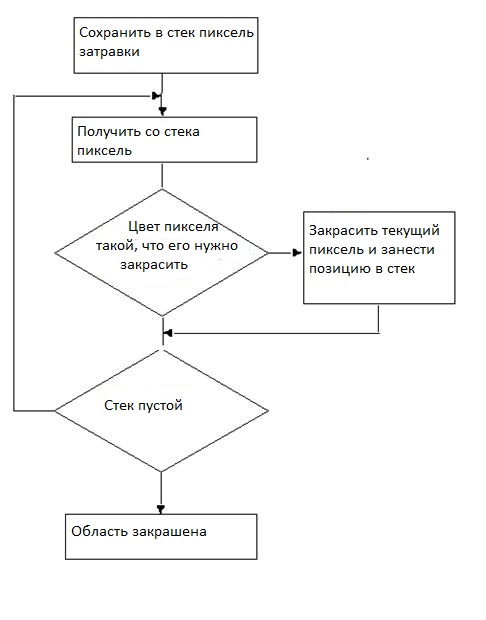
Для определения точек, принадлежащих области, в том числе, а также найти количество точек области, надо использовать тот или иной алгоритм заполнения односвязной области. Рассмотрим один из них.Простой алгоритм заполнения с затравкой.
Используя стек, можно разработать простой алгоритм заполнения связной области. Стек - это просто массив или другая структура данных, в которую можно последовательно помещать значения и из которой их можно последовательно выбирать. Когда новые значения добавляются или помещаются в стек, все остальные значения опускаются вниз на один уровень. Когда значение удаляются или вытягиваются из стека, другие значения всплывают или поднимаются вверх на один уровень. Такой стек называетсо стеком прямого действия или стеком с дисциплиной обслуживания "первым пришел, последним вышел" (LIFO). Простой алгоритм заполнения с затравкой можно представить в следующем виде:Простой алгоритм заполнения Затравка(х, у) видает затравочный пиксел. Push - процедура, которая вкладывает пиксел в стек. Pop - процедура, которая вынимает пиксел со стека. Піксел(х, у) = Затравка(х, у) Push Пиксел(х, у) ; инициализация стека While (стек не пустой) Pop Пиксел(х, у) ; вынимаем пиксел со стека If Пиксел(х, у) <> Нов_значения then Пиксел(х, у) = Нов_значения End if Проверка, нужно ли вкладывать соседние пиксели в стек If (Пиксел(х + 1, у) <> Нов_значения and Пиксел(х + 1, у) <> Гран-значения)then Push Пиксел (х + 1, у) If (Пиксел(х, у + 1) <> Нов_значения and Пиксел(х, у + 1) <> Гран_значения)then Push Пиксел (х, у + 1) If (Пиксел(х - 1, у) <> Нов_значения and Піксел(х - 1, у) <> Гран_значения)then Push Пиксел (х - 1, у) If (Пиксел(х, у - 1) <> Нов_значения and Пиксел(х, у - 1) <> Гран_значения)then PushПиксел (х, у - 1) End If EndWhile
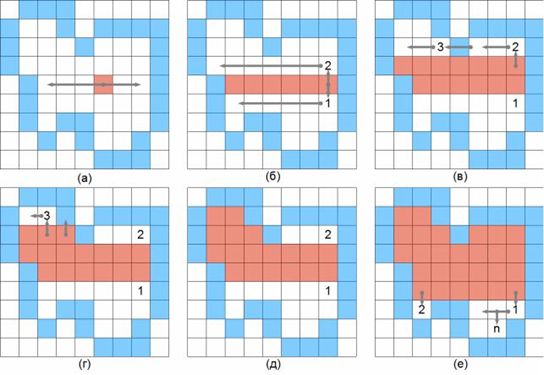

Алгоритм водораздела.
Сегментация водотоков - алгоритм, вдохновленный природой, имитирующий затопления водой топографического рельефа.
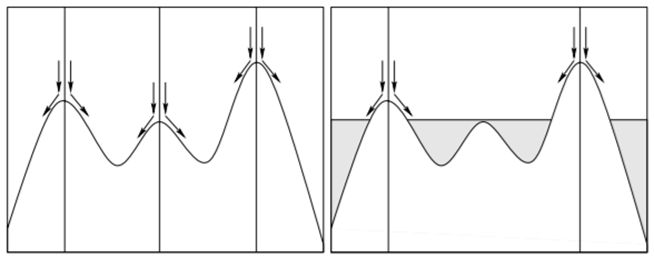

Проиллюстрируем шаг за шагом алгоритм водораздела на изображение Lena.
Шаг первый – бинаризация.


Данный процесс представляет собой сопоставление переднего плана бинарного изображения с расстоянием от ближайшего препятствия или фонового пикселя. Этот процесс позволяет убрать небольшие или вытянутые области, сохраняя региональные центры.



Суперпиксельная сегментация.
Суперпиксельная сегментация реализует разбиение изображения на множество мелких фрагментов (суперпикселей), представляющие собой относительно однородные группы расположенных рядом точек. Каждый суперпиксель есть потенциально атомарным регионом (фрагментом) изображения, то есть, все входящие в него пиксели рассматриваются при дальнейшей обработке как единое целое. При этом суперпиксели не обязательно должны иметь правильную форму и, естественно, всегда есть определенное число ошибок, допускаемых при стремлении разбить изображение на однородные фрагменты. Основное требование к суперпиксельной сегментации заключается в следующем: пиксели внутри каждого суперпикселя должны быть максимально похожи, а пиксели, которые находятся в разных суперпикселях, должны в определенной степени отличаться. Данная задача может решаться принципиально различными способами. Рассмотрим один из лучших методов суперпиксельнои сегментации- SLIC (Simple Linear Iterative Clustering).Простая линейная итерационная кластеризация (SLIC) является адаптацией k -среднего для генерации суперпикселей с двумя важными отличиями:
- Оптимизация количеству расчетов расстоянии значительно сокращается путем ограничения пространства поиска на область, пропорциональное размеру суперпикселя. Это делает сложность линейной по количеству точек N и независимым от числа суперпикселив k.
- Мера взвешенной расстоянии сочетает в себе цветовую и пространственную близость, одновременно обеспечивая контроль за размером и компактностью суперпикселей.
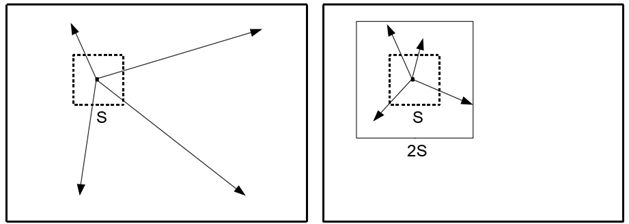
SLIC простой в использовании и понимании. По умолчанию единственным параметром алгоритма является параметр k - ожидаемое количество суперпикселов примерно равного размера. Для цветных изображений в цветовом пространстве CIELAB процедура кластеризации начинается с этапа инициализации, где k стартовых центров кластеров \(C_i = [l_i a_i b_i x_i y_i]^T \) выбираются на регулярной сетке, с шагом в S пикселей. Для получения примерно одинаковых размеров суперпикселей, интервал сетки выбирается равным \(S = \sqrt {\frac {N} {k}} \). На каждой итерации центры перемещаются на место, соответствующее наименьшей позиции градиента в окрестности 3 × 3 пикселя \ [ G (x, y) = \| I (x + 1, y) -I (x-1, y) \|^2 + \| I (x, y + 1) -I (x, y-1) \|^2, \] где \ (I (x, y) \) lab вектор, соответствующий пикселю с позицией (x, y) и \(\| \cdot \| \) норма \(L_2 \).
Это делается для того, чтобы избежать центрирования суперпикселя по краю, и чтобы уменьшить вероятность совпадения суперпикселей с зашумленных пикселем. Поскольку ожидаемая пространственная протяженность суперпикселя является областью примерно размера S × S, поиск подобных точек осуществляется в области 2S × 2S вокруг центра суперпикселей.Как только каждый пиксель ассоциируется с ближайшим центром кластера, шаг обновления регулирует центры кластера как среднего вектора \([L a b x y]^Т \) всех точек, принадлежащих кластеру.
Норма \(L_2 \) используется для вычисления остаточной ошибки E между новыми местами центра кластера и предварительным центрами кластера. Шаги назначения и обновления можно повторять итерационно, пока ошибка не совпадает, но для большинства изображений достаточно 10 итераций.
Алгоритм SLIC суперпиксельной сегментации / Инициализация / Инициализация центров кластеров Ck = [lk ak bk xk yk]T - виборка пикселов на регулярной сетке с шагом S. Переместить центры кластера в наинизшую позицию градиєнта в окрестности 3 × 3. Поставить метку l (i) = −1 для каждого пикселя i. Установить рассояние d (i) = ∞ для каждого пикселя i. repeat / Назначения / for каждого кластерного центра Ck do for каждого пикселя i в области 2S × 2S около Ck do Найти расстояние D между Ck и i. if D < d (i) then множество d (i) = D множество l (i) = k end if end for end for / Обновление / Вычислить новые центры кластеров. Нахождение остаточной ошибки E. until E ≤ порога
Мера расстояния.
Суперпиксели SLIC соответствуют кластерам в пространстве плоскости цвета labxy. Это создает проблему при определении меры D, которая может быть не очевидной. D - расстояние между пикселем i и центром кластера \(C_k \) в алгоритме. Цвет пикселя представлен в цветовом пространстве CIELAB [l a b] T . Положение позиции пикселя [x y] T , с другой стороны, может принимать диапазон значений в зависимости от размера изображения.Просто определения D как евклидово расстояние в пятимерном пространстве labxy приведет к несоответствию в кластеризации. Для больших суперпикселив пространственные расстояния превосходят цветовую близость, предоставляя более относительное значение пространственной близости, чем цвет. Это производит компактные суперпиксели, не хорошо придерживаются границ изображения. Для мелких суперпикселив верно обратное.
Чтобы объединить две расстоянии в единую меру, необходимо нормализовать близость цвета и пространственную близость по их соответствующими максимальными расстояниями в пределах кластера.Пусть \[ d_c=\sqrt{(l_j-l_i)^2+(a_j-a_i )^2+(b_j-b_i )^2 }, \] \[ d_s=\sqrt{(x_j-x_i )^2+(y_j-y_i )^2 }, \] \[ D'=\sqrt{\left(\frac{d_c}{N_c} \right)^2+\left(\frac{d_s}{N_s} \right)^2 }. \] Максимальное пространственное расстояние, ожидаемое в пределах данного кластера должно соответствовать интервалам выборки, \(N_s = S = \sqrt {\frac {N} {K}} \). Определение максимального расстояния цвета \(N_c \) не так просто, поскольку цветовые расстояния могут существенно отличаться от кластера к кластеру и от изображения к изображению. Этой проблемы можно избежать, заменив \(N_c \) на константу m , тогда \[ D'=\sqrt{\left(\frac{d_c}{m} \right)^2+\left(\frac{d_s}{S} \right)^2 }. \] что упрощает измерения расстояния. На практике используется значение расстояния \[ D=\sqrt{\left(d_c \right)^2+m^2\left(\frac{d_s}{S} \right)^2 }. \] Определяя D таким образом, m также позволяет взвешивать относительную важность между цветовой сходством и пространственной близостью. Когда m является большим, пространственная близость является более важной и результирующие суперпиксели более компактными (то есть они имеют более низкое соотношение области к периметру). Когда m является малым, полученные суперпиксели плотнее прилипают к границам изображения, но имеют меньший размер и форму. При использовании цветового пространства CIELAB параметр m изменяется в диапазоне \(m \in [1, 40] \), но, как правило, выбирается значение m = 20 . В некоторых случаях в качестве характеристики расстояния используется значенния \[ D=d_c+\frac{d_s}{S} m,m\in [1,20]. \] Уравнение может быть приспособлено для изображений в градациях серого путем настройки \[ d_c=\sqrt{(l_j-l_i )^2 }. \] Приведем примеры суперпиксельной сегментации для различных параметров.
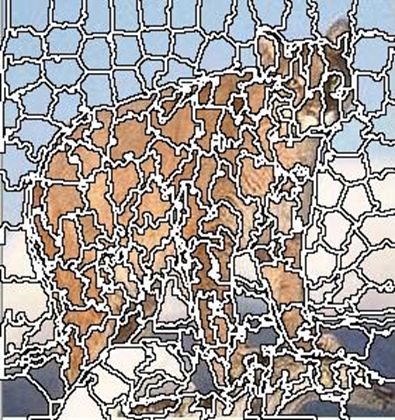 |  | |
| Количество сегментов 200, m=10. | Количество сегментов 200, m=40. |
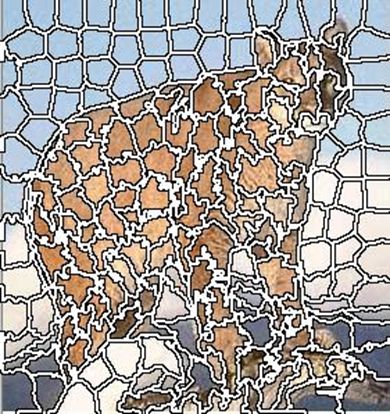 |  | |
| Количество сегментов 200, m=20. | Количество сегментов 20, m=20. |
Текстурная сегментация по фрактальными характеристиками.
Важной задачей анализа изображений является формирование сегментов по текстуре областей. Проблема сложная и плохо формализуется. Один из подходов для решения такого рода задачи состоит в том, что фрагменты изображения анализируются с точки зрения самоподобия, то есть с точки зрения фрактальности.Фракталы и фрактальная размерность.
Термин фрактал был предложен Бенуа Мандельброт (B. Mandelbrot) в 1975 году для обозначения нерегулярных самоподобных математических структур. Основное определение фрактала, данное Мандельбротом, звучал так: "фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому". Стоит признать, что это определение, в силу своей нестрогости, не всегда верно. Можно привести много примеров самоподобных объектов, не являющихся фракталами, например, железнодорожные пути сходящихся к горизонту.В простейшем случае небольшая часть фрактала содержит информацию о всем фрактале. Строгое определение самоподобных множеств было дано Дж. Хатчинсоном (J. Hutchinson) в 1981 году. Он назвал множество самоподобным, если оно состоит из нескольких компонентов, подобных всему этому множеству, то есть каждый компонент получается аффинным преобразованием.
Однако самоподобнисть - это хотя и необходимое, но далеко не достаточное свойство фракталов. Ведь нельзя же, в самом деле, считать фракталом точку, или плоскость, расчерченную клетками. Главная особенность фрактальных объектов заключается в том, что для их описания недостаточно «стандартной» топологической размерности, которая, как известно, для линии равна 1, для поверхности 2, и т.д. Фракталам характерна геометрическая «изрезанность». Поэтому используется специальное понятие фрактальной размерности, введенное Ф. Хаусдорфом (F. Hausdorf) и А.С. Безиковичем. Применительно к идеальным объектам классической евклидовой геометрии она давала те же численные значения, что и топологическая размерность, однако новая размерность имела более тонкую чувствительность ко всякого рода несовершенствам реальных объектов, позволяя различать и индивидуализировать то, что когда-то было безликое и неразличимое. Размерность Хаусдорфа - Безиковича как раз и позволяет измерять степень «изрезанности». Размерность фрактальных объектов не является целым числом, характерным для привычных геометрических объектов. Вместе с тем, в большинстве случаев фракталы напоминают объекты, которые плотно занимают реальное пространство, но не используют его полностью.Пусть имеется множество G в евклидовом пространстве размерности r . Это множество покрывается кубиками той же размерности, при этом длина ребра любого кубика не превышает некоторого значения δ, то есть \(\delta_i \lt \delta \).
Вводится зависящая от некоторого параметра d и δ сумма по всем элементам покрытия: \[ \ell_d(\delta)=\sum_i\delta_i^d. \] Определим нижнюю грань данной суммы: \[ L_d=\inf\sum_i\left\{\left.\delta_i^d\right|\delta_i\lt\delta\right\} \] При уменьшении максимальной длины δ, если параметр d будет достаточно большой, будет выполняться \[ \lim_{\delta\to 0}L_d(\delta)\to \infty. \] При некотором достаточно малом значении параметра d будет выполняться: \[ \lim_{\delta\to 0}L_d(\delta)\to 0. \] Промежуточное, критическое значение \(\ sigma \), для которого выполняется: \[ \lim_{\delta\to 0}L_d(\delta)= \left\{ \begin{array}{ll} 0, & \hbox{якщо }d\gt \sigma,\\ \infty, & \hbox{якщо }d\lt \sigma, \end{array} \right. \] и называется размерностью Хаусдорфа-Безиковича (или фрактальной размерностью). Для простых геометрических объектов размерность Хаусдорфа-Безиковича совпадает с топологическрй (для отрезка 1, для квадрата 2, для куба 3 и т.д.)Несмотря на то, что размерность Хаусдорфа-Безиковича с теоретической точки зрения определена безупречно, для реальных фрактальных объектов расчет этой размерности является достаточно затруднительным. Поэтому вводится несколько упрощеный показатель - емкостная размерность \(d_c \).
При определении этой размерности используются кубики с гранями одинакового размера. В этом случае, естественно, справедливо: \(L_d(\delta)=N(\delta)\delta^{dc}\),де N(δ) - количество кубиков, покрывающих область G. Путем логарифмирования и перехода к пределу, при уменьшении грани кубика, получаем: \[ d_c=-\lim_{\delta\to 0}\frac{\log{N(\delta)}}{\log{\delta}}, \] если этот предел существует. Следует отметить, что в большинстве численных методов определения фрактальной размерности используется именно \(d_c \). При этом необходимо учитывать, что всегда справедливо условие: \(\sigma \ le d_c \). Для регулярных же подобных фракталов емкостная размерность и размерность Хаусдорфа-Безиковича совпадают, поэтому терминологически их часто различают и говорят просто о фрактальной размерности объекта. К сожалению классический подход позволяет оценить фрактальный размер объектов на плоскости, например, береговую линию, а с тем, чтобы оценить двумерный объект, таким есть изображение, то существуют большие проблемы. Но все не так плохо, существуют некоторые подходы, которые и рассмотрим.Методы оценки фрактальности цветных / полутоновых изображений.
В основе оценки цветных / полутоновых изображений лежит тот факт, что любое серое (полутоновое, grayscale) или цветное изображение можно представить как некоторую поверхность, где низменностям отвечают "темные" пиксели, а пикам - горам соответствуют "светлые" пиксели.Рассмотрим несколько методов.
Метод Triangular Prism Surface Area.
Метод TPSA предназначен для обработки полутоновых (grayscale) изображений.
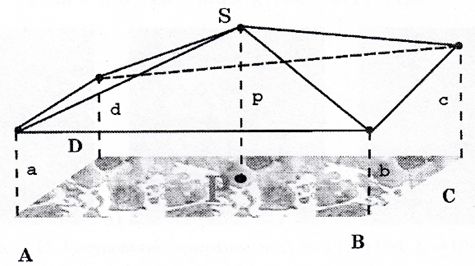
Алгоритм состоит в следующем.
Рассматривается центральный пиксель Р и его окружение - квадрат ABCD, линии между величинами a, b, с, d, р - образуют 4 треугольника с вершиной S и площадью: \[ S_p=\sum_{i=1}^4Str_i,Str_i=F(x_i,y_i,r), \] где \(S_p \) - площадь фигуры, \(Str_i \) - площадь i-го треугольника \(i = 1..4, x_i, y_i \) - координаты точек (вершины i-го треугольника), r - сторона квадрата ABCD .Подобная процедура повторяется для всех точек изображения. Для фиксированного r площади всех фигур формируют одну общую площадь A. .
Затем r увеличивается, и процедура повторяется. Наклон s графика A (r) в логарифмическом масштабе используется для определения фрактальной размерности: \(D_ {tP} = 2 s \).Данный метод, при исследовании цветных изображений, позволяет оценивать размерность каждого цветового канала RGB или отдельно размерность "яркости" изображения.
Meтод 2D Variation Procedure.Метод 2D Variation предназначен для обработки бинарных (binary) и полутоновых (grayscale) изображений.
Находим минимальный и максимальный уровни серого в пределах каждой квадратной области со стороной r. Таким образом, определяются двухмерная минимальная и максимальная функции для каждого шага решетки. Потом для всего изображения определяется разница объема между минимальными и максимальными функциями.
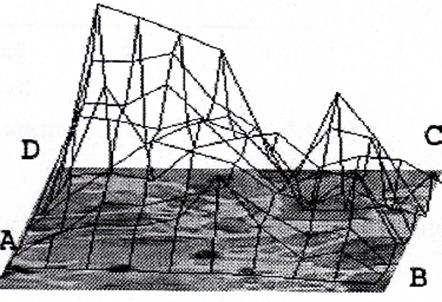
Тогда \(V(r)=r^sconst\), где V - «разностный» объем фигури r - шаг сетки, S- фрактальная размерность.
Подобная процедура повторяется для всех пикселей изображения, затем r увеличивается, и процедура повторяется.Наклон s графика V(r) в логарифмическом масштабе используется для определения фрактальной размерности: \[ D_{2D}=3-\frac{s}{2}. \] Данный метод при работе с цветными изображениями также как и TPSA позволяет оценивать как размерность каждого цветового канала RGB отдельно, так и размерность "яркости" изображения.
Броуновская размерность.Еще одним методом оценки фрактальной размерности полутоновых изображений является броуновская размерность, которая пропорциональна экспоненте Херста (Hurst`s exponent) D=3-H.
Параметр Н можно вычислить статистически из закона дисперсии, используя свойства броуновского движения: \[ H=-\frac{\log\left(\sigma_{\Delta R}(\Delta I)\right)}{\log(\Delta R)} \] \(\sigma_{\Delta R}(\Delta I)\) - средне квадратичное отклонение приростов, то есть разница яркости в точках \(R+\Delta R\) и \(R\), \(\Delta I=I(R+\Delta R)-I(R)\), \(R\) - координаты точки.Алгоритм вычисления выглядит следующим образом: для всех точек определяются приращения яркости \(\Delta I\) в \(\Delta R\)-окрестности, для полученного массива приростов находим среднее отклонение \(\sigma_{\Delta R}(\Delta I)\), потом изменяем \(\Delta R\) и повторяем предыдущие шаги.
Наклон графика зависимости \(\sigma_{\Delta R}(\Delta I)\) от \(\Delta R\) в логарифмических координатах дает нам величину Н.Данный метод при работе с цветными изображениями также как и TPSA и 2D Variation Procedure позволяет оценивать как размерность каждого цвета RGB отдельно, так и размерность "яркости" изображения.
Таким образом, после того, как каждому пикселю поставим в соответствие фрактальную размерность, после фрагментации шкалы фрактальной размерности можно провести соответствующую сегментацию изображения.
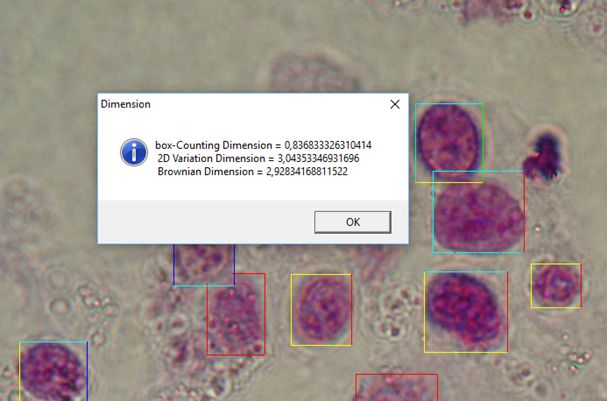
Относительно практического использования фрактальных характеристик, то информацию об этом можно найти здесь.
Используемые изображения
 |
|
Наиболее популярная женщина среди специалистов по компьютерной графике – Lena Soderberg (с обложки журнала Playboy за ноябрь 1972 г.) |
 |
| Костел святого Николая (Каменское) конец ХIХ ст. |
 |
| Cougar. Когуар или пума. Кошка, красивая до смерти. |
 |
| Изображение Superfood. Мечта вегана. |
 |
| Клетки букального эпителия. (Архив цитопрепаратов крови и костного мозка, отдел онкогематологии ИЕПОР НАНУ). |
Полезная литература.
- Falconer K.J. The geometry of fractal sets . — Cambridge: Cambridge university press , 1995. — 162 p.
- Falconer K.J. Fractal Geometry. Mathematical Foundations and Applications . — Chichester: John Wiley & Sons , 2003. — 337 p.
- Geng Weidong. The Algorithms and Principles of Non-photorealistic Graphics. Artistic Rendering and Cartoon Animation / Weidong Geng . – Hanzhou: Springer, 1995 . – 373 p.
- Francus P. Image Analysis, Sediments and Paleoenvironments . — Dordrecht: Springer, 1998. — 472 p.
- Leondes C.T. Image Processing and Pattern Recognition / C.T.Leondes . — NY: AP, 1998. — 407 p.
- Sangwine S.J. The Color Image Processing Handbook / S.J.Sangwine, R.E.Horne . — Dordrecht: Springer, 2004. — 330 p.
- Анисимов Б.В. Распознавание и цифровая обработка изображений: Учеб. пособие для студентов вузов / Б.В. Анисимов, В.Д. Курганов, В.К. Злобин . – М.: Высш.шк., 1983 .– 295 с.
- Бутаков Е.А. Обработка изображений на ЭВМ / Е.А. Бутаков, В.И. Островский, И.Л. Фадеев . – М.: Радио и связь, 1987 .– 238 с.
- Введение в контурный анализ, приложения к обработке изображений и сигналов / Под ред. Я.А.Фурмана. – М.:Физматлит, 2003.-592 с.
- Грузман И.С., Киричук В.С., Косых В.П., Перетягин Г.И., Спектор А.А. Цифровая обработка изображений в информационных системах: Учеб. пособие. — Новосибирск.: Изд-во НГТУ, 2003. — 352 с.
- Гонсалес Р. Цифровая обработка изображений / Р. Гонсалес, Р. Вудс . – М.: Техносфера, 2005 .– 1070 с.
- Гонсалес Р. Цифровая обработка изображений в среде MATLAB/ Р. Гонсалес, Р. Вудс, С. Эддингс . – М.: Техносфера, 2006 .– 616 с.
- Гришенцев А.Ю. Методы и модели цифровой обработки изображений / А.Ю.Гришенцев, А.Г.Коробейников .— СПб: Изд. Политех.ун-та, 2014 .— 190 с.
- Доля П.Г. Методы обработки изображений. Учебное пособие / П.Г. Доля . – Харьков.: Изд. ХНУ, 2013 .– 46 с.
- Ежова К.В. Моделирование и обработка изображений. Учебное пособие / К.В. Ежова . – СПб.: НИУ ИТМО, 2011 .– 93 с.
- Кроновер Р.М. Фракталы и хаос в динамических системах. - M. ПОСТМАРКТ, 2000. - 350 с.
- Лигун А.А. Асимптотические методы восстановления кривых / А.А.Лигун, А.А.Шумейко .— К.: Изд. Института математики НАН Украины, 1997 .— 358 с.
- Лигун А.О. Комп'ютерна графіка (Обробка та стиск зображень) / А.О.Лигун, О.О.Шумейко .— Дніпропетровськ: Біла К.О., 2010 .— 114 с.
- Методы компьютерной обработки изображений/ Под ред. В.А.Сойфера.- М.:Физматлит, 2003.-784 с.
- Новейшие методы обработки изображений / Под ред. А.А.Потапова.- М.:Физматлит, 2008.-496 с.
- Павлидис Т. Алгоритмы машинной графики и обработки изображений / Т. Павлидис . – М.: Радио и связь, 1986 .– 400 с.
- Прэтт У. Цифровая обработка изображений. Кн. 1 / У. Прэтт . – М.: Мир, 1982 .– 312 с.
- Таранцев И.Г. Компьютерная графика. Метод.пособие / И.Г.Таранцев . – Новосиб.: Изд. гос.ун-та, 2009 . – 60 с.
- Федотов А.А. Методы компьютерной обработки биомедицинских изображений в среде MATLAB: учеб. пособие / А.А. Федотов, С.А. Акулов, А.С. Акулова. – Самара: Изд-во СГАУ, 2015. – 88 с.
- Фисенко В.Т., Фисенко Т.Ю., Компьютерная обработка и распознавание изображений: учеб. пособие. — СПб: СПбГУ ИТМО, 2008. — 192 с.
- Фурман Я.А. Цифровые методы обработки и распознавания бинарных изображений / Я.А.Фурман, А.Н.Юрьев, В.В.Яшин .— Красноярск: Изд. Краснояр. ун-та, 1992 .— 248 с.
- Хуанг Т. Обработка изображений и цифровая фильрация / Т.Хуанг .— М: Мир, 1979 .— 318 с.
- Шумейко А.А. Интеллектуальный анализ данных (Введение в Data Mining) / А.А.Шумейко, С.Л.Сотник .— Днепропетровск: Белая Е.А., 2012 .— 212 с.
- Яне Б. Цифровая обработка изображений. — М.: Техносфера, 2007. — 584 с.
- Яншин В.В. Обработка изображений на языке Си для IBM PC: Алгоритмы и программы / В.В.Яншин, Г.А.Калинин .— М: Мир, 1994 .— 241 с.
- Ярославский Л.П. Введение в цифровую обработку изображений. — М.: Сов. радио, 1979. — 312 с.
- https://www.codeproject.com/Articles/751744/Image-Segmentation-using-Unsupervised-Watershed-Al
- SLIC Superpixels Compared to State-of-the-art Superpixel Methods / [R.Achanta, A.Shaji, K.Smith та ін.] // Journal of latex class files .— 2011 .— №1(6) .— C.1-8.
- Bandara Ravimal Image Segmentation using Unsupervised Watershed Algorithm with an Over-segmentation Reduction Technique
