 Векторизация элементов растрового изображения
Векторизация элементов растрового изображения
Классически для выявления контуров используется свертка матрицы яркости \(Y=\left\{y_{i,j}\right\}_{i=1,j=1}^{W,H}\) c оператором Собела: \begin{equation}\label{1} G^S_x=\left( \begin{array}{ccc} -1 & 0& 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \\ \end{array} \right)\otimes Y, G^S_y=\left( \begin{array}{ccc} 1 & 2& 1 \\ 0 & 0 & 0 \\ -1 & -2 & 1 \\ \end{array} \right)\otimes Y. \end{equation} или с оператором Превита: \begin{equation}\label{2} G^P_x=\left( \begin{array}{ccc} -1 & 0& 1 \\ -1 & 0 & 1 \\ -1 & 0 & 1 \\ \end{array} \right)\otimes Y, G^P_y=\left( \begin{array}{ccc} 1 & 1& 1 \\ 0 & 0 & 0 \\ -1 & -1 & 1 \\ \end{array} \right)\otimes Y. \end{equation} Обозначим через \(G=\left\{g_{i,j}\right\}_{i=1,j=1}^{W,H}\) ( W, H – размеры матрицы) матрицу для выбранного оператора, элементы которой имеют вид: \begin{equation}\label{3} g_{i,j}=\|grad(i,j)\|=\sqrt{\left(g^x_{i,j}\right)^2+\left(g^y_{i,j}\right)^2}. \end{equation} Для того, чтобы найти особо контрастные места, которые принадлежат векторизации, к матрице G применяется бинаризация по порогу. Таким образом, находим бинарную матрицу \(Bin=\left\{b_{i,j}\right\}_{i=1,j=1}^{W,H}\), у которой \begin{equation}\label{4} b_{i,j}= \left\{ \begin{array}{ll} 1, & \hbox{ если }g_{i,j}\gt \varepsilon, \\ 0, & \hbox{ в противном случае.} \end{array} \right. \end{equation} где \(\varepsilon\)– порог бинаризации.
Каждый элемент матрицы Bin дополнительно анализируется на предмет принадлежности к региону интереса (ROI-Region Of Interest) - например, удаляются изолированные точки, которые, скорее всего, относятся к шумам.
Одной из главных проблем данного подхода является выбор порога бинаризации (один из которых рассмотрен в разделе, посвященном пространственной фильтрации изображений). Особенно эта проблема становится актуальной, если на картинке присутствуют элементы с разным уровнем освещения.
Анализ связных компонент.
Данный метод заключается в сегментации бинарного изображения на связные регионы и их последующий анализ. Обычно бинарным изображением является матрица Bin, полученная в результате построения границ объектов.Будем называть точки \((x_1,y_1)\) и \((x_2,y_2)\) соседними, если они удовлетворяют условию связности, а именно, для 4-х связной области условие связности имеет вид: \[ x_1-x_2=0,|y_1-y_2|=1 \] или \[ |x_1-x_2|=1,y_1-y_2=0. \] Для 8-ми связной: \begin{equation}\label{5} |x_1-x_2|\le 1,|y_1-y_2|\le 1 \end{equation} На рис. 1 наглядно проиллюстрировано понятие связности.
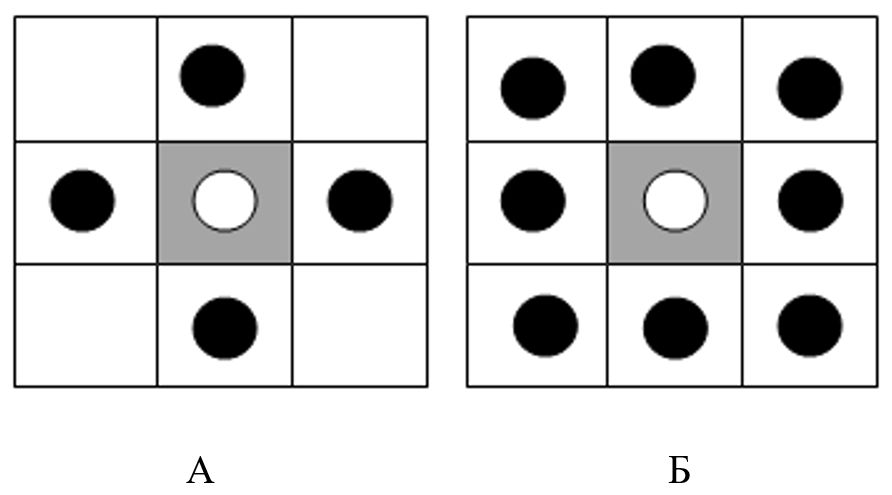
Рис. 1 А) 4-х связаная область; Б) 8-ми связаная область.
Существуют различные алгоритмы построения связных множеств, например, такие как: алгоритм заполнения с «затравкой» (рассмотрен в разделе, посвященном сегментации изображений), порядковый линейный алгоритм и др.
Конечным шагом работы алгоритма является анализ различных характеристик, которыми обладают полученные связные множества: отсечения шума, отсечение таких графических элементов, как внутренние изображения и т.д. Очевидно, что в данном подходе многое зависит от того бинарного изображения, которое анализируется для построения связных компонент.
Изъятие линий из изображения.
Контуром будем называть области изображения с высокой концентрацией информации, контур мало зависит от цвета и яркости. Выявление контуров позволяет перейти из двумерного пространства изображения в пространство контуров, позволяет снизить вычислительную и алгоритмическую сложность анализа изображения, повысить качество восстановленного изображения при меньших размерах, а также провести более детальный анализ объекта, описанного контуром.Традиционно для выявления контуров используются подходы, опирающиеся на информацию о значениях градиента и на совпадениях с шаблоном. Обе методики оценивают локальное значение градиента и его проекции. Отличие в том, что для оценки градиента обычно используются фильтры, которые позволяют отлавливать перепады в двух ортогональных направлениях, например, фильтры Собела (\ref{1}), Превіта (\ref{2}), а также фильтр Робертса: \[ G^R_x=\left( \begin{array}{cc} 0 & 1 \\ -1 & 0 \\ \end{array} \right)\otimes Y, G^R_y=\left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \\ \end{array} \right)\otimes Y. \] где \(Y=\left\{y_{i,j}\right\}_{i=1,j=1}^{W,H}\) матрица освещенности.
Для подхода совпадения с шаблоном характерно использование фильтров, которые проявляют нужные критерии и дают необходимую погрешность совпадения. Контрастные перепады на картинке находятся в точках максимального значения градиента \(\|grad(i,j)\|\) (см. рис. 3). Обычно для отделения контрастных точек используется некоторое пороговое значение \(\varepsilon\) \[ \|grad(i,j)\|\gt \varepsilon. \] Выбор порога - важная часть определения перепадов, от которой зависит толщина и непрерывность контуров. На данный момент среди подобных методов выделяют фильтр Кенни.
Основные этапы алгоритма Кенни:
- Сглаживание. Фильтр Кенни чувствителен к шумам на изображении, поэтому первоначальная матрица сглаживается с помощью фильтра Гаусса: \[ Gauss= \left( \begin{array}{ccccc} 2 & 4 & 5& 4 & 2 \\ 4 & 9 & 12 & 9 & 4 \\ 5 & 12 & 15 & 12 & 5 \\ 4 & 9 & 12 & 9 & 4 \\ 2 & 4 & 5 & 4 & 2 \\ \end{array} \right)\otimes Y. \]
- Поиск градиентов. Находим градиенты, согласно выбранным фильтрам (Собела, Прeвита, Робертса). Для того чтобы отследить линии с наклоном, фильтры расширяются диагональными операторами, чтобы выявить линии под соответствующим углом: \(0,\pi/4,\pi/2,3\pi/4\).
- Подавление немаксимумов. В качестве контуров отмечаются только те точки, в которых находится локальный максимум градиента в направлении вектора градиента.
- Двойная пороговая фильтрация. Высокий порог используется для выявления сильных контуров, низкий порог - для присоединения к сильным контуров, менее четких, но которые являются их частью.
- Трассировки областей неоднозначности. Заглушаются слабые контуры, не связанные с сильными.
 |  |
| А | Б |
| Рис.2. Применение фильтра Кенни к тестовому изображению "Bicycle". | |
| А) Оригинальное тестовое изображение; | Б) Изображение после применения фильтра Кенни. |
Векторное описание линий.
Для того чтобы выделенные контуры улучшили свою структуру и лучше поддавались аналитическому описанию, классически к полученному контуру применяют морфологические операции вида - наращивание, эрозия, замыкание, размыкание (см. раздел, посвященный пространственным фильтрам).Конечной целью обработки контуров является векторизация. Под векторизацией мы будем понимать способ представления объектов и изображений, основанный на использовании элементарных геометрических объектов: точки, линии, ломаные, сплайны, многоугольники.
Преобразование Хафа.
Одним из самых известных методов выявления прямой является преобразование Хафа. Отметим, что преобразования Хафа можно обобщить на случай поиска других примитивов, таких как дуг окружностей и др.В преобразовании Хафа используется представление прямой в виде: \(r=x\cos\theta+y\sin\theta\), где \(\theta\in [0,\pi],r\in \mathbb{R}\).
Тогда, \(F(r,\theta,x,y)=x\cos\theta+y\sin\theta\) соотношение, задающее семейство прямых.
Через каждую точку \((x,y)\) изображения можно провести множество прямых с различными параметрами \(r,\theta\). Каждой точке на изображении \(r_0,\theta_0\) пространства \(r,\theta\) можно поставить в соответствие счетчик, значение которого соответствует количеству точек (x,y), лежащих на прямой \(r_0=x\cos\theta_0+y\sin\theta_0\). Точка \(r_0,\theta_0\), в которой достигается максимальное значение счетчика, описывает параметры искомой прямой (на рис. 3 наиболее темная точка - негатив максимального значения счетчика).
Чтобы описать компьютерную реализацию, перейдем к дискретному случаю пространства \(r,\theta\). Таким образом, введем сетку на \(r,\theta\) пространстве и поставим в соответствие каждой клетке \([r_i,\theta_i]\times [r_{i+1},\theta_{i+1}]\) счетчик количества точек (x,y), удовлетворяющих уравнению \[ r=x\cos\theta+y\sin\theta,\theta\in [\theta_i,\theta_{i+1}],r\in [r_i,r_{i+1}]. \]
 |  |
| А | Б |
| Рис. 3. Демонстрация преобразования Хафа; | |
| А) Оригинальный набор точек; | Б) Негатив отображения пространства Хафа – чем темнее точка, тем большее значение соответствующего счетчика. |
Если на изображении имеется несколько прямых, их можно получить с помощью перестановки величин счетчиков. Однако если прямые на картинке должны сложиться в ломаную линию, после преобразования Хафа могут появиться разрывы, так как непрерывность звеньев ломаной в преобразовании никак не учитывается. Поэтому для этого случая предпочтительный вариант непосредственного приближения множества точек ломаными. В этом случае мы имеем дело с кусочно-линейной аппроксимацией.
Метод кусочно-линейной аппроксимации заключается в замене заданного множества точек ломаной с одной или несколькими узлами.
Опишем построение «почти» оптимального восстановления кривой в метрике Хаусдорфа (визуальной метрике) (см. [19]).
Описание асимптотически оптимальной ломаной.
Пусть задано упорядоченное множество связанных точек \((x_i,y_i)\), тогда для заданного порога ε > 0 число звеньев асимптотически оптимальной интерполяционной ломаной вычисляется по формуле: \[ m=\left[\frac{1}{4\sqrt{2\varepsilon}}\sum_{i=0}^{n-1}\Delta\ell_{i+1/2}(K_i+K_{i+1})\right]+1, \] где [α] - целая часть числа α, \[ K_i=\sqrt{\frac{|x_i''y_i'-x_i'y_i''|}{\sqrt{\left(x_i'\right)^2+\left(y_i'\right)^2}}},\\ x_{i+1/2}'=\frac{x_{i+1}-x_i}{\Delta\ell_{i+1/2}}, y_{i+1/2}'=\frac{y_{i+1}-y_i}{\Delta\ell_{i+1/2}},\\ \Delta\ell_{i+1/2}=\sqrt{(x_{i+1}-x_i)^2+(y_{i+1}-y_i)^2},\\ x_i'=\frac{x_{i+1/2}'+x_{i-1/2}'}{2},y_i'=\frac{y_{i+1/2}'+y_{i-1/2}'}{2},\\ x_i''=2\frac{x_{i+1/2}'-x_{i-1/2}'}{\Delta\ell_{i+1/2}+\Delta\ell_{i-1/2}}, y_i''=2\frac{y_{i+1/2}'-y_{i-1/2}'}{\Delta\ell_{i+1/2}+\Delta\ell_{i-1/2}},\\ x'_{-1/2}=2x'_{1/2}-x'_{3/2},y'_{-1/2}=2y'_{1/2}-y'_{3/2}, x'_{n+1/2}=2x'_{n-1/2}-x'_{n-3/2}, y'_{n+1/2}=y'_{n-1/2}-y'_{n-3/2}. \] А координаты узлов ломаной \(t_j,j=0,1,...,m\) выбираются из условия: \[ \sum_{i=0}^{t_j}\Delta\ell_{i+1/2}(K_i+K_{i+1}+m^{-2/3})\le \frac{j}{m}\sum_{i=0}^{m}\Delta\ell_{i+1/2}(K_i+K_{i+1}+m^{-2/3})\le \sum_{i=0}^{t_j+1}\Delta\ell_{i+1/2}(K_i+K_{i+1}+m^{-2/3}). \] Таким образом, имеем асимптотически оптимальную интерполяционную ломаную с таким числом узлов и их расположением, чтобы обеспечить заданную погрешность приближения ε.Очевидно, что не все кривые могут быть эффективно приближены ломаными с достаточно малым количеством узлов. Для описания сложных кривых разработана методика приближения сплайнами.
Функция S(t), определенная на отрезке [a,b], называется полиномиальным сплайном порядка m с узлами \(a\le x_0\lt ...\lt x_n\le b\), если на каждом из отрезков \([x_{j-1},x_j]\), \(S(t)\) является алгебраическим полиномом степени, не более m. Если в точке \(x_j,(j=0,...,n)\) функции \(S(t),S'(t),..,S^{(m-k)}(t)\) непрерывные, а производная \(S^{(m-k+1)}\) в точке \(x_j\) имеет разрыв, число k называют дефектом сплайна. Множество \(\{x_0,x_1,...,x_n\}\) называется сеткой узлов сплайна, а точки \(x_j\) - узлами или точками склейки сплайна.
Пример сплайна 2-го порядка (параболический сплайн) приведен на рисунке.
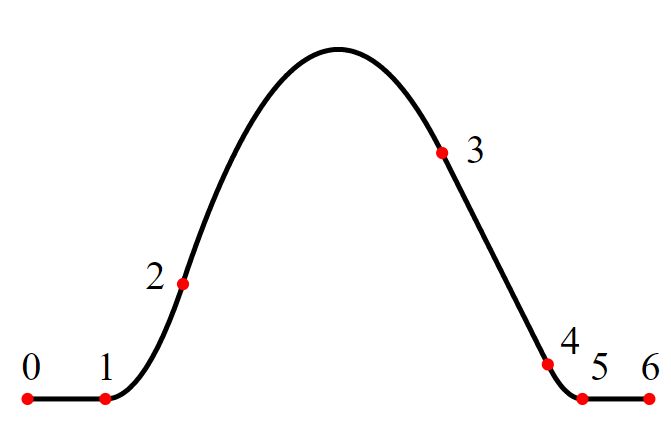
Рис.4. Пример приближения функции сплайном 2-го порядка.
Для равномерного разбиения \(a\le h\lt 2h\lt ...\lt (n-1)h\le b\) для точек \(M_{i},M_{i+1/2},M_{i+1}\) квадратичный сплайн Безье будет иметь вид: \[ sb\left(\left\{M_{i},M_{i+1/2},M_{i+1}\right\},t\right)=M_i(1-\tau)^2+2\,M_{i+1/2}\tau(1-\tau)+M_{i+1}\tau^2, \] где \(\tau=(t-ih)h^{-1},t\in [ih,(i+1)h]\).
Однако для сплайнов Безье обратной стороной их простоты является достаточно высокая ошибка приближения. Качество приближения сплайнами Безье такое же, как у интерполяционных ломаных.
Локализация слабоконтрастных линий.
Как уже было отмечено, проблема локализации линий, четко выраженных на картинке, достаточно хорошо изучена и существуют алгоритмы выявления таких линий основанные, например, на фильтрах Собела, Превитта, Кенни. Сложность определения слоя линий возрастает с усложнением фона, на которых эти линии находятся. Рассмотрим задачу выделения в отдельный слой слабоконтрастных линий с нечеткой структурой относительно фона прилегающих точек. Такие линии, можно увидеть на рис. 5.

Рис.5. Тестовый пример "Bicycle". На рис 5 А и рис. 5.б приведены примеры линий,
контрастных в окружающем фоне, на рис. 5. В и рис. 5 Г примеры линий,
слабоконтрастных на окружающем фоне.
Этап 1. Формирование множества точек фона;
Этап 2. Формирование множеств контрастных по фону.
Этап 1. Формирование точек фона.
Понятие локального фона является ключевым и интуитивно под фоном понимается множество точек изображения, каждая из которых имеет достаточное число соседей с похожей освещенностью. При этом не очень заметные линии на изображении состоят из точек, которые по своей освещенности очень близки к яркости соседних точек фона. В дальнейшем в рамках описания алгоритма, это понятие будет формализовано.
Будем работать с освещенностью изображение, представляющее собой числовую матрицу \(Y=\left\{y_{i,j}\right\}_{i=1,j-1}^{W,H}\).
Через \(C^R_{i,j}=\left\{(\nu,\mu):(i-\nu)^2+(j-\mu)^2\le R^2\right\}\) обозначим окрестность точки (i,j) радиусом R (в нашем случае рассматривался R=3) и каждой точке изображения поставим в соответствие среднюю освещенность окрестности \begin{equation}\label{6} b^R_{i,j}=\frac{1}{\sum\left\{1\left|(\nu,\mu)\in C^R_{i,j}\right.\right\}}\sum\left\{y_{\nu,\mu}\left|(\nu,\mu)\in C^R_{i,j}\right.\right\} \end{equation} Для заданного \(\delta\gt 0\) определим множество \[ \Re(\delta)=\left\{(i,j):\left||y_{i,j}-b^R_{i,j}|\lt \delta\right.\right\}. \] Все точки этого множества будем называть первичными точками фона по порогу δ. При определении множества первичных точек фона, использовались точки, в дальнейшем не вошли в это множество, поэтому надо переопределить понятие окрестности, опираясь на информацию только о точках с R(δ) \[ \tilde{C}^R_{i,j}=\left\{(\nu,\mu)\left|(\nu,mu)\in C^R_{i,j},(\nu,\mu)\in \Re(\delta)\right.\right\}. \] Используя уточненное понятие окрестности первичной точки фона, заново найдем значение освещенности фона в точке \((i,j)\) \[ \tilde{b}^R_{i,j}=\frac{1}{\sum\left\{1\left|(\nu,\mu)\in \tilde{C}^R_{i,j}\right.\right\}}\sum\left\{y_{\nu,\mu}\left|(\nu,\mu)\in \tilde{C}^R_{i,j}\right.\right\} \] Значение освещенности точек, принадлежащих линиям, слабоконтрастных по окружающему фону, более существенно отличаются от значений яркости фона, чем значение точек, не лежащих на подобных местах. При выделении линий естественно требовать, чтобы точки, которые могут им принадлежать, не участвовали в формировании освещенности фона. Для этой цели построим следующую процедуру. Для каждой точки окрестности \(\tilde{C}^R_{i,j}\) найдем ошибку описания ее освещенности средним значением фона \[ e^{(i,j)}_{\nu,\mu}=\left|y_{\nu.\mu}-\tilde{b}^R_{i,j}\right|,(\nu,\mu)\in \tilde{C}^R_{i,j} \] и построим множество точек \(M^R_{i,j}\), которое состоит из Θ процентов точек \((\nu,\mu)\in \tilde{C}^R_{i,j}\), для которых значение ошибок \(e^{(i,j)}_{\nu,\mu}\) максимальные (например, \(\Theta\approx 20\%\) ). Вычислим новые средние значения, удалив точки с максимальным отклонением: \[ \tilde{b}^M_{i,j}=\frac{1}{\sum\left\{1\left|(\nu,\mu)\in \tilde{C}^R_{i,j}\setminus M^R_{i,j}\right.\right\}}\sum\left\{y_{\nu,\mu}\left|(\nu,\mu)\in \tilde{C}^R_{i,j}\setminus M^R_{i,j}\right.\right\} \] Аналогично предыдущему утверждению, собственно фоновыми точками будем считать точки, удовлетворяющие условию: \begin{equation}\label{7} \left|y_{i,j}-\tilde{b}_{i,j}^{M^R_{i,j}}\right|\lt\varepsilon,(i,j)\in\Re(\delta), \end{equation} где \(\varepsilon\gt 0\) – параметр, регулирующий количество точек фона.
Все точки, удовлетворяющие условию (\ref{7}), образуют множество точек фона\(\tilde{\Re}(\Theta,\delta)\).
Этап 2. Формирование множеств точек, контрастных на фоне.
Точки, принадлежащие множеству \(P^\delta=\Re(\delta)\setminus\tilde{\Re}(\Theta,\delta)\), будем называть точками, контрастными на фоне. Все эти точки "подозрительные" на предмет формирования линий. Через \(\left\{P_k^\delta\right\}_{k=1}^m\) обозначим множества связных точек изображения, то есть точек, для которых выполняется условие 8-ми связности(\ref{5}) двох точек \((i,j)\) и \(\nu,\mu\).Мерой множества A будем называть величину \[ mes(A)=\sum\left\{1|(i,j)\in A\right\} \] Отметим, что в множество \(P^\delta\) могут попасть точки, содержащие шум. Поэтому прежде чем приступить к формированию линий на базе множества \(\left\{P_k^\delta\right\}_{k=1}^n\), необходимо провести очистку изображения от шумов. Не останавливаясь на этом вопросе подробно, отметим, что фильтрация данных от шума является важной и интересной задачей. Существуют различные алгоритмы очистки, в данном случае можно воспользоваться методом удаления элементов с малой мерой. Таким образом, в результате получаем множество \(\left\{P_k^\delta\right\}_{k=1}^m\) связных точек, которое будем называть слабо контрастными (нечеткими) линиями относительно фона.
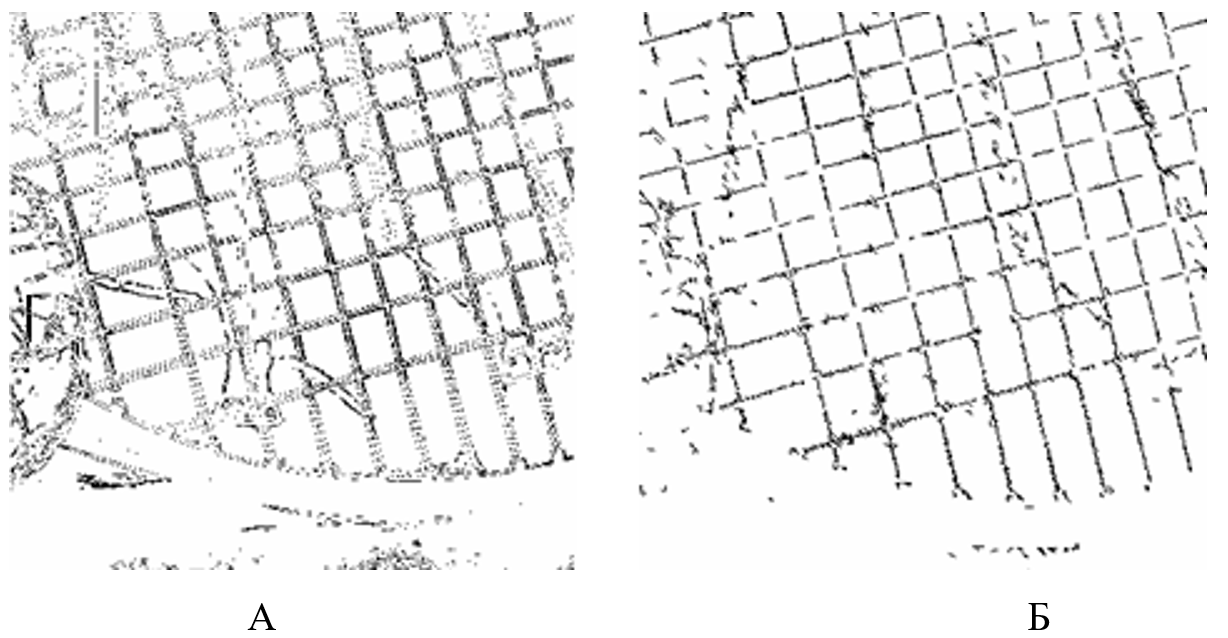
6. А) Выделение нечетких линий с помощью фильтров Собела;
Б) Выделение нечетких линий с помощью описанного подхода.
Формирование суперлиний.
Сложность топологической структуры множеств \(\left\{P_k^\delta\right\}_{k=1}^m\) не позволяет реализовать их эффективную обработку, поэтому является актуальным описание множеств \(\left\{P_k^\delta\right\}_{k=1}^n\) объектами более простой конструкции - суперлиниями, чему посвящены дальнейшие построения.Так как любое связное множество может быть представлено в виде подмножества объединения кругов, то \(P^\delta_k\subset\bigcup_{(i,j)\in B_k}C^{R_{i,j}}_{i,j}\). Связное множество\(B(B^\delta_k)=\left\{(i_\nu,j_\nu)\right\}_{\nu=1}^{N_k}\) будем называть каркасом множества \(P^\delta_k\), если оно дает решение следующей экстремальной задачи \begin{equation}\label{8} \left\{ \begin{array}{l} \sum_{(i,j)\in B_k}mes\left(C^{R_{i,j}}_{i,j}\right)\to\min,\\ P^\delta_k\subset\bigcup_{(i,j)\in B_k}C^{R_{i,j}}_{i,j}. \end{array} \right. \end{equation} Каркас множества описывает геометрическое поведение множества в целом, поэтому для описания \(\left\{P_k^\delta\right\}_{k=1}^m\) воспользуемся их представлением через каркасы. Заметим, что получение каркаса множества с использованием решения задачи (\ref{8}) трудоемкое и, вообще говоря, не требуется для корректного описания множества. Поэтому далее рассмотрим способ построения множества, близкого к каркасу, конструирование которого существенно проще.
Граничной точкой множества будем называть точку, с которой граничит, хотя бы одна точка, не принадлежащая этому множеству.
Контуром будем называть упорядоченную замкнутую последовательность граничных точек, в котором ν и (ν + 1) -я точка связные, но каждая точка граничит не более чем с двумя граничными точками.
Под однопиксельной линией будем понимать связное множество, каждая точка (пиксель) которой имеет не более 3 соседей из множества (рис. 7Б). Под строго однопиксельные линией будем понимать такую однопиксельные линию, в которой удаление любой точки, кроме конечной, приводит к потере связности (рис. 7А).
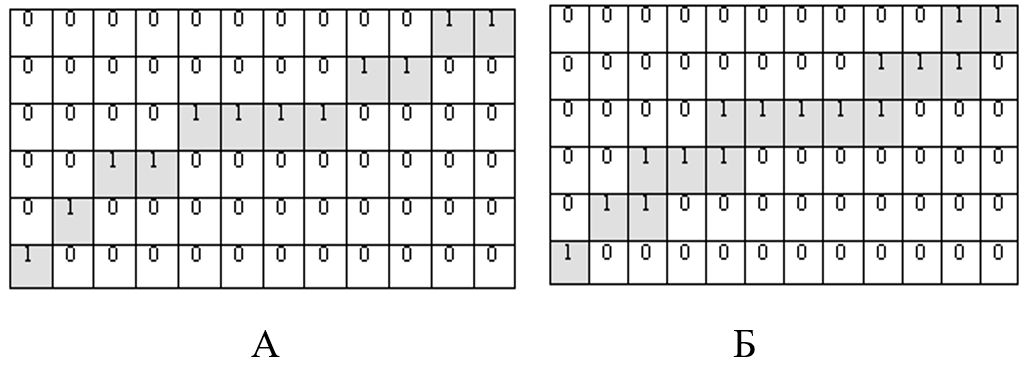
Рис. 7. А) Строго однопиксельные линия; Б) однопиксельные линия.
Этап 1. Построение маски множества.
Поставим в соответствие множеству точек A матрицу \(\{a_{i,j}\}_{i=1,j=1}^{W^A,H^A}\), где
\[
a_{i,j}=\left\{
\begin{array}{ll}
1, & \hbox{ } (i,j)\in A;\\
0, & \hbox{ } (i,j)\notin A.
\end{array}
\right.
\]
Этап 2. Нахождение контура множества.
Задаем правило обхода граничных точек. Для построения контура будем обходить каждую предельную точку в фиксированном направлении, например, в положительном,
и при этом каждый элемент контура \(p_k\) будем характеризовать парой точек \(V(p_k)\) и \(U(p_k)\), где \(V(p_k)\) координаты k-й точки контура,
а \(U(p_k)\)- координаты точки, к которой при заданном обходе была добавлена k-та точка, то есть \(U(p_k)=V(p_{k-1})\).
Построение контура начинается с произвольной предельной точки множества A. Продвигаясь по направлению контура, присоединяем очередной элемент.
Матрица \(\{a_{i,j}\}_{i=1,j=1}^{W^A,H^A}\) отражает влияние каждой точки на формирование контура. Добавляя k-й элемент в контур, увеличиваем на единицу значимость точки
в матрице \(\{a_{i,j}\}_{i=1,j=1}^{W^A,H^A}\) с координатами \(V(p_k)_x,V(p_k)_y\). По определению контур является замкнутым, поэтому процесс должен завершиться, когда в
контур будет добавлен элемент, совпадающий с первым, то есть \(V(p_k)=V(p_1)\). Но для корректной обработки ситуации петель этого сравнения недостаточно,
поэтому необходимо сравнивать все характеристики элемента, то есть и\(U(p_k)\). Учитывая то, что первый элемент не владеет информацией о \(U(p_1)\),
Будем считать, что контур построен, если выполнены следующие условия:
\[
V(p_k)=V(p_2),\\U(p_k)=U(p_2).
\]
Последние два добавленных элемента необходимы для алгоритмизации остановки формирования контура, то есть не должны влиять на формирование \(\{a_{i,j}\}_{i=1,j=1}^{W^A,H^A}\).
Этап 3. Удаление множества контура из изображения.
После построения контура анализируем влияние каждой предельной точки на формирование контура. Заметим, что одна и та же предельная точка может присутствовать в
нескольких элементах контура, в этом случае она существенна для связности множества А и не может быть удалена.
Для того чтобы эффективно анализировать вхождения каждой предельной точки в элементы контура, не используя дополнительный поиск, была введена матрица
\(\{a_{i,j}\}_{i=1,j=1}^{W^A,H^A}\). Исходя из ее значений, легко проанализировать влияние граничных точек на формирование контура.
Элементы \(a_{i,j}\) могут принимать значения:
1 – если точка не входит в контур;
>2 – если точка входит в контур не один раз, а, значит, ее удаление приводит к нарушению связности множества A.
2 – если точка, требует дополнительного анализа на удаление.

Рис.8. Пример поэтапного удаления контура множества.
 |  |
| A | Б |
| Рис.9. А) Фрагмент нечетко выраженных линий; | Б) Этот же фрагмент после обработки. |
Однако каркас в чистом виде еще не является той линией, которую удобно приближать аналитически. В каркасе обычно присутствуют сечения, и визуально выделяются длинные линии, из которых он состоит.
Суперлиниейбудем называть множество строго однопиксельные линий, объединенных в местах пересечения. Первым шагом построения является получение мест пересечений. Будем называть узловой точкой строго однопиксельной линии такую точку \(x_k,y_k\), для которой выполняется условие: \[ \sum\left\{1\left|(x_i,y_i)\in D^1_{x_k,y_k},(x_i,y_i)\in\{P_k\}_{k=1}^m\right.\right\}\gt 3. \] Как показала практика для формализации связей каркаса недостаточно опираться только на определение узловых точек. На рис. 10. представлены «хорошие» узловые точки - в этом случае сечение явно выражается в одной узловой точке. На рис. 11. ситуация иная - один сечение характеризуется 4-мя узловыми точками.

Рис. 10. Примеры «хороших» узловых точек.
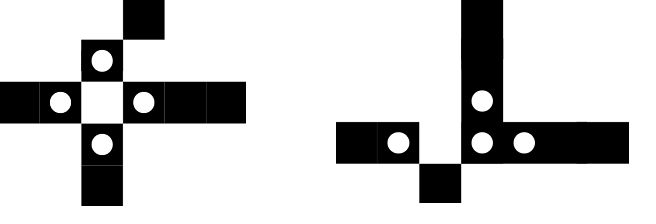
Рис. 11. Примеры «плохих» узловых точек.
Узлом будем называть связанную множество точек, опирается на узловые точки и содержат не более чем K НЕ узловых точек. Параметр K регулирует допустимое распространение узла. Обычно K = 3.
Из каждого узла выходят фрагменты каркаса.
Фрагментом будем называть строго однопиксельную линию, которая не является узлом, и имеет или две узловые точки, или две конечные точки, или один узел и одну конечную точку: \(F_i=\left\{p^i_k\right\}_{k=1}^{N_i}\), где \(N_i\)- количество точек в фрагменте, \(p_1^i,...,p_{N_i}^i\) узловые или конечные точки.
Таким образом, каркас может быть представлен из узлов и фрагментов каркаса, и является строго однопиксельными линиями: \[\bigcup_i^{N_f}F_i\subset \{P_k\}_{k-1}^m,\] где \(N_f\)– количество фрагментов каркаса.
Будем считать, что в одну линию могут быть объединены два фрагмента, которые исходят из одного узла, если они похожи по градиенту. Формализуем это утверждение.
Пусть из узла выходят m фрагментов \(\{F_k\}_{k=1}^m\). Считаем, что точки каждого фрагмента упорядочены от текущего до следующего узла или конечной точки. Это не представляет сложности, учитывая то, что фрагменты - строго однопиксельные линии. Первые N (рекомендуемое значение N = 5) точек каждого фрагмента аппроксимируем с помощью прямой. Таким образом, сравнение градиента фрагментов сведем к сравнению параметров соответствующих прямых.
Так как расстояние от точки \((x_i,y_i)\) до прямой \(x\cos\varphi+y\sin\varphi+c=0\) равно \[\varepsilon_i=\left|x_i\cos\varphi+y_i\sin\varphi+c\right|,\] то прямую, наиболее близкую к точкам \(\left\{(x_i,y_i)\right\}_{i=1}^N\), будем искать из условия: \begin{equation}\label{9} \sum_{i=1}^N\left|x_i\cos\varphi+y_i\sin\varphi+c\right|^2\to\min_{\varphi,c}. \end{equation} Не останавливаясь подробно, выпишем решение \(\tilde{\varphi}\) этой экстремальной задачи \[ \tilde{\varphi}=\frac{1}{2}\mathrm{arctg}\left(2\frac{\sum_{\nu=1}^Nx_\nu y_\nu-\frac{1}{N}\sum_{\nu=1}^Nx_\nu \sum_{\nu=1}^Ny_\nu} {\sum_{\nu=1}^Ny_\nu^2-\frac{1}{N}\left(\sum_{\nu=1}^N y_\nu\right)^2-\sum_{\nu=1}^Nx_\nu^2+\frac{1}{N}\left(\sum_{\nu=1}^N x_\nu\right)^2}\right)+\frac{\pi k}{4}. \] Таким образом, каждому фрагменту \(F_k\) поставим в соответствие \(\tilde{\varphi}_k\). Для того чтобы упорядочить степени сходства всех возможных пар фрагментов в узле, введем расстояние \(d(\varphi_1,\varphi_2)\) с учетом того, что \(\tilde{\varphi}+\pi\) также является решением экстремальной задачи.
Отложим каждый угол на единичной окружности.
Пусть функция \(\mathrm{Pos}(\varphi)\) возвращает координаты угла на единичной окружности в декартовой системе координат. Таким образом, расстояние между параметрами двух прямых находим по формуле \[ d(\varphi_1,\varphi_2)=\min\left\{d_E(\mathrm{Pos}(\varphi_1),\mathrm{Pos}(\varphi_2)),d_E(\mathrm{Pos}(\varphi_1),\mathrm{Pos}(\varphi_2+\pi))\right\}, \] где функция \(d_E\)– евклидово расстояние, то есть \[ d_E((x_1,y_1),(x_2,y_2))=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}. \] Построим следующую матрицу расстояний между всеми возможными парами фрагментов \[ W=\left( \begin{array}{cccc} \infty & d(\varphi_1,\varphi_2) & \cdots & d(\varphi_1,\varphi_m) \\ d(\varphi_2,\varphi_1) & \infty& \cdots & d(\varphi_2,\varphi_m) \\ \vdots & \vdots & \infty & \vdots \\ d(\varphi_m,\varphi_1) & d(\varphi_m,\varphi_2) & \cdots & \infty \\ \end{array} \right) \] Значение элементов по диагонали установим равными бесконечности, так на этих местах расположено значение расстояния между одной и той же прямой, а нас интересуют только возможные пары.
Пара фрагментов \(F_i\) и \(F_j\) объединяется в одну суперлинии, если \[w_{i,j}=\min_{i,j=1,...,m}(W).\] Считая, что \(F_i\) и \(F_j\) нашли пару, устанавливаем в соответствующих столбцах и строках матрицы значения элементов равными бесконечности. И снова строим новую пару. И так до тех пор, пока не останется элементов матрицы равных бесконечности или такой элемент будет один. Объединяем все фрагменты в линию, если они образуют пары и имеют общий узел.
Заметим, что полученные линии носят явно дискретный характер, поэтому следующим этапом будет их сглаживание, что позволит находить их дифференциальные характеристики.
Для простоты дальнейшего рассмотрения, следующие выкладки будем рассматривать на примере одной суперлинии, которая представляет собой множество \(\{p_i\}_{i=1}^n\).
Пополним выходные данные \(p_i=(x_i,y_i),i=1,...,n\) точками, чтобы алгоритмы работали корректно для всех точек линии \begin{equation}\label{10} p_0=\frac{1}{3}(4\,p_1+p_2-2\,p_3), p_{n+1}=\frac{1}{3}(4\,p_n+p_{n-1}-2\,p_{n-2} \end{equation} и вычислим сглаженые значение \begin{equation}\label{11} p^*_i=p_i+\alpha\Delta^2p_i=p_i+\alpha(p_{i-1}-2\,p_i+p_{i+1}), \end{equation} где \(\alpha\in (0,1/3]\) (если \(\alpha=1/3\), то получим медианное сглаживание).
После этого проведем переприсвоение \(p_i=p^*_i,i=1,2,...,n\) и повторим процесс сглаживания до тех пор пока заданного \(\varepsilon\gt 0\) и \(\forall i=1,2,...,n\) не выполнится условие: \[ \left(x'_{i+1/2}\right)^2+ \left(y'_{i+1/2}\right)^2=1+\varepsilon, \] где \begin{equation}\label{12} x'_{i+1/2}=\frac{x_{i+1}-x_i}{\Delta\ell_{i+1/2}},y'_{i+1/2}=\frac{y_{i+1}-y_i}{\Delta\ell_{i+1/2}},\\ \Delta\ell_{i+1/2}=\sqrt{(x_{i+1}-x_i)^2+(y_{i+1}-y_i)^2},\\ x'_{-1/2}=2\,x'_{1/2}-x'_{3/2},x'_{n+1/2}=2\,x'_{n-1/2}-x'_{n-3/2},\\ y'_{-1/2}=2\,y'_{1/2}-y'_{3/2},y'_{n+1/2}=2\,y'_{n-1/2}-y'_{n-3/2}. \end{equation} Таким образом, результатом работы данного этапа является набор сглаженных суперлиний.
Аналитическое описание суперлиний.
Суперлинию \(\{p_i\}_{i=1}^n\) будем описывать в зависимости от ее геометрической формы. Будем использовать такие типы суперлиний, как прямые, ломаные, кривые. Для определения принадлежности суперлинии к тому или иному типу будем применять дискретный аналог кривизны в каждой точке.Обозначим через \(\Phi_i\) дискретное значение кривизны в точке \(x_i,y_i\), которая вычисляется по формуле: \[ \Phi_i=\frac{\left|x''_iy'_i-x'_iy''_i\right|}{\left((x'_i)^2-(y'_i)^2\right)^{3/2}},i=0,1,...,n, \] где \[ x_i'=\frac{x_{i+1/2}'+x_{i-1/2}'}{2},y_i'=\frac{y_{i+1/2}'+y_{i-1/2}'}{2},\\ x_i''=2\frac{x_{i+1/2}'-x_{i-1/2}'}{\Delta\ell_{i+1/2}+\Delta\ell_{i-1/2}}, y_i''=2\frac{y_{i+1/2}'-y_{i-1/2}'}{\Delta\ell_{i+1/2}+\Delta\ell_{i-1/2}}, \] а недостающие значения производных определяются в соответствии с формулами (\ref{12}).
Таким образом, для точек \(\{p_i\}_{i=1}^n\), которые образуют собой суперлинии, получаем набор \(\{\Phi_i\}_{i=1}^n\), который будет критерием выбора аппарата приближения.
Этап 1. Аппроксимация прямой.
Будем считать, что если для заданного порога δ>0 выполняется неравенство \(\max_i\Phi_i\le\delta\), то линия достаточно хорошо описывается прямой
\(x\cos\varphi+y\sin\varphi+c=0\), которая находится из условия регрессии.
В этом случае:
\[
\varphi=\frac{1}{2}\mathrm{arctg}\left(2\frac{\sum_{\nu=1}^Nx_\nu y_\nu-\frac{1}{N}\sum_{\nu=1}^Nx_\nu \sum_{\nu=1}^Ny_\nu}
{\sum_{\nu=1}^Ny_\nu^2-\frac{1}{N}\left(\sum_{\nu=1}^N y_\nu\right)^2-\sum_{\nu=1}^Nx_\nu^2+\frac{1}{N}\left(\sum_{\nu=1}^N x_\nu\right)^2}\right)+\frac{\pi k}{4}.
\]
и
\[
c=-\frac{1}{n+1}\left(\sum_{\nu=0}^nx_\nu\cos\varphi+\sum_{\nu=0}^ny_\nu\sin\varphi\right).\]
Если условие \(\max_i\Phi_i\le\delta\) не выполняется, то на следующем шаге сделаем попытку описать суперлинии ломаной.
Этап 2. Аппроксимация ломаной.
При использовании ломаных нужно, чтобы требуемая точность описания линии давала ломаная с малым числом звеньев, например, не более 10 звеньев.
То есть если для множества точек \(p^*_i,i=1,2,...,n\) недостаточно ломаной не более чем из 10 звеньями, значит, для приближения нужно
использовать другой аппарат.
Для построения такой ломаной использовался алгоритм асимптотически оптимального восстановления кривой в метрике Хаусдорфа (визуальной метрике).
Приведем алгоритм построения оптимальной ломаной (с точки зрения минимизации узлов при заданной погрешности). Этот алгоритм позволяет гарантированно получить
ломаную с наименьшим числом узлов.
Пусть \((x_i,y_i), i=1,2,...,n\) упорядоченные точки, соответствующие некоторому контуру Γ, который необходимо описать и ε- допустимая ошибка.
Через \((x_1,y_1)\) обозначим стартовую точку, в роли которой возьмем любую точку с ε-окрестности точки \((x_1,y_1)\), например, именно эту точку.
Построим следующий итерационный процесс - пусть, прежде всего, i=2 и ν=1. Через точки \((x_i,y_i)\) и \((x_\nu,y_\nu)\)
построим прямую и найдем точку
\((x_j,y_j)\) , удаленную от этой прямой на расстояние, равное допустимой погрешности, то есть
\[
\frac{|(y_j-y_i)(x_\nu-x_i)-(x_j-x_i)(y_\nu-y_i)|}{\sqrt{(x_\nu-x_i)^2+(y_\nu-y_i)^2}}\le\varepsilon\le
\frac{|(y_{j+1}-y_i)(x_\nu-x_i)-(x_{j+1}-x_i)(y_\nu-y_i)|}{\sqrt{(x_\nu-x_i)^2+(y_\nu-y_i)^2}}.
\]
Проекцию точки \((x_j,y_j)\) на прямую \((y-y_j)(x_\nu-x_i)=(x-x_j)(y_\nu-y_i)\) обозначим через \((x^*,y^*)\) и длина звена ломаной будет равна
\[
h_\nu=\sqrt{(x^*-x_\nu)^2+(y^*-y_\nu)^2}.
\]
Далее считаем i = i +1 и повторяем этот процесс, пока не найдем максимальное значение \(h_\nu\). После этого, в роли стартовой точки возьмем \(x_\nu,y_\nu\)
и этот процесс будем повторять до тех пор, пока j ≤ n. В результате получим ломаную, которая описывает данную кривую с заданной погрешностью ε и с наименьшим числом звеньев
(то есть с наименьшим числом информативных характеристик).
Если в результате полученное число звеньев достаточно мало, например, не более десяти, то вместо искомой кривой будем использовать эту ломаную.
Если же точек \(x_\nu,y_\nu\) много, то для описания кривой используем более сложный аппарат.
Этап 3. Аппроксимация сплайнами Безьє.
Для аналитического описания суперлинии, которая не может быть приближена прямой или ломаной с данной точностью, будем использовать аппарат приближения Безье -
кривыми. Рассмотрим одну конструкцию сплайнов Безье, которая, не меняя локальных свойств аппроксимации Безье, для равномерного разбиения позволяет получить
инструмент приближения, который асимптотически совпадает с интерполяционным сплайном минимального дефекта.
Известно, что для \(t\in [ih,(i+1)h]\) любой параболический сплайн минимального дефекта по разбиению \(ih,i\in Z\) можно записать в виде (см.[17])
\begin{equation}\label{13}
s_2(t)=\sum_ic_iB_{2,h}\left(t-h\frac{2i+1}{2}\right)=
c_{i-1}B_{2,h}\left(t-h\frac{2i-1}{2}\right)+c_iB_{2,h}\left(t-h\frac{2i+1}{2}\right)+c_{i+1}B_{2,h}\left(t-h\frac{2i+3}{2}\right),
\end{equation}
где \(B_{2,h}(t)\)– параболический B- сплайн по решетке с шагом h (см., например, здесь ).
Для непрерывной функции \(f\) положим \(f_{i+1/2}=f((i+0.5)h)\) и \(f_i=f(ih)\). В данном разделе показано, что если
\[
\tilde{c}_i=f_{i+1/2}-\frac{1}{8}\Delta^2f_{i+1/2},
\]
тогда сплайн
\begin{equation}\label{14}
\tilde{s}_2(f,t)=\sum_{i=-1}^n\tilde{c}_iB_{2,h}\left(t-h\frac{2i+1}{2}\right)
\end{equation}
асимптотически совпадает с интерполяционным сплайном, то есть
\[
\tilde{s}_2(f,(i+0.5)h)=f_{i+1/2}-\frac{1}{64}\Delta^4f_{i+1/2},
\]
и при этом, если \(f\in C^3\), то для \(t\in [ih,(i+1)h]\)
\begin{equation}\label{15}
f(t)-\tilde{s}_2(f,t)=\frac{h^3}{3}\tau(1-\tau)(\tau-0.5)f^{(3)}(t)+O(h^3),
\end{equation}
где \(\tau=\frac{t-ih}{h}\).
Сплайны вида (\ref{14}) достаточно удобны и просты, однако в ряде программных средств для графического отображения используются параболические сплайны Безье.
Построим такую конструкцию сплайнов Безье, которые будут совпадать с почти интерполяционными сплайнами (\ref{14}).
Получение такой конструкции сплайнов Безье позволяет повысить эффективность встроенных графических функций.
Расчет опорных точек Безье кривой.
Для \(t\in [ih,(i+1)h]\) и точек \(M_i,M_{i+1/2},M_{i+1}\) сплайн Безье имеет вид \[ sb(\{M_i,M_{i+1/2},M_{i+1}\},t)=M_i(1-\tau)^2+2\,M_{i+1/2}\tau (1-\tau)^2+M_{i+1}\tau^2. \] Тогда производная имеет вид \[ sb'(\{M_i,M_{i+1/2},M_{i+1}\},t)=\frac{2}{h}(-M_i(1-\tau)+M_{i+1/2}(1-2\,\tau)+M_{i+1}\tau) \] и \[ sb'(\{M_i,M_{i+1/2},M_{i+1}\},ih)=\frac{2}{h}(-M_i+M_{i+1/2}),\\ sb'(\{M_i,M_{i+1/2},M_{i+1}\},(i+1)h)=\frac{2}{h}(M_{i+1}-M_{i+1/2}). \] Кроме того, \[ sb(\{M_i,M_{i+1/2},M_{i+1}\},(i+0.5)h)=\frac{1}{4}(M_i+2\,M_{i+1/2}+M_{i+1}). \] Замечая, что \[ \tilde{s}'_2(f,ih)=\frac{1}{8\,h}(11\,f_{i+1/2}-f_{i+3/2}-11\,f_{i-1/2}+f_{i-3/2}),\\ \tilde{s}'_2(f,(i+1)h)=\frac{1}{8\,h}(11\,f_{i+3/2}-f_{i+5/2}-11\,f_{i+1/2}+f_{i-1/2}), \] и \[ \tilde{s}'_2(f,(i+0.5)h)=\frac{1}{16}f_{i+3/2}-\frac{1}{64}f_{i+5/2}+\frac{29}{32}f_{i+1/2}+\frac{1}{16}f_{i-1/2}-\frac{1}{64}f_{i-3/2}, \] выпишем условия непрерывности сплайна и его производной, приводящие к системе: \[ \left\{ \begin{array}{l} sb'(\{M_i,M_{i+1/2},M_{i+1}\},ih)= \tilde{s}'_2(f,ih);\\ sb'(\{M_i,M_{i+1/2},M_{i+1}\},(i+1)h)= \tilde{s}'_2(f,(i+1)h);\\ sb'(\{M_i,M_{i+1/2},M_{i+1}\},(i+1/2)h)= \tilde{s}'_2(f,(i+1/2)h). \end{array} \right. \] Решая эту систему, получаем \[ \tilde{M}_i=-\frac{1}{16}f_{i-3/2}+\frac{9}{16}f_{i-1/2}+\frac{9}{16}f_{i+1/2}-\frac{1}{16}f_{i+3/2},\\ \tilde{M}_{i+1/2}=-\frac{1}{8}f_{i+3/2}+\frac{5}{4}f_{i+1/2}-\frac{1}{8}f_{i-1/2},\\ \tilde{M}_{i+1}=-\frac{1}{16}f_{i-1/2}+\frac{9}{16}f_{i+1/2}+\frac{9}{16}f_{i+3/2}-\frac{1}{16}f_{i+5/2}. \] Сплайн Безье \(sb(\{M_i,M_{i+1/2},M_{i+1}\},t)\) будет совпадать с почти интерполяционным параболическим сплайном минимального дефекта.Приведем один пример использования векторизации растровых изображений с целью уменьшения размера данных. Ниже приведен фрагмент векторного слоя, на котором алгоритм автоматически выбрал подходящие варианты приближения фрагментов линий.
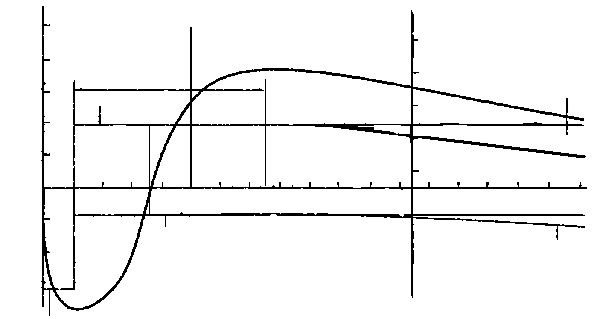
Рис. 12. Оригинальный фрагмент в формате TIF (3530 байт).
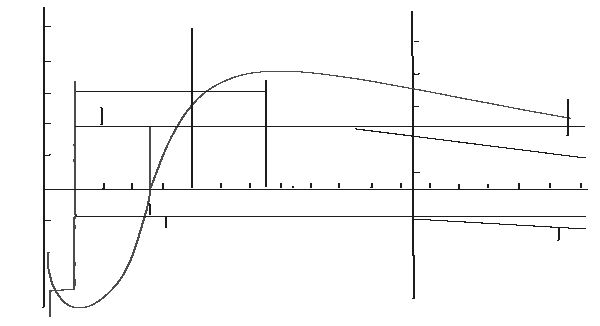
Рис. 13. Векторизований фрагмент (800 байт).
Полезная литература.
- Asymptotically Optimum Recovery of Smooth Contours by Bezier Curve / A.A.Ligun, A.A.Shumeiko, S.P.Radzevich, E.D.Goodman // Computer Aided Geometric Design .— 1998 .— №15 .— C.495-506.
- Canny John, A Computational Approach to Edge Detection, Pattern Analysis and Machine Intelligence / John Canny // IEEE Transactions on .– Nov. 1986 .– 679 – 698 p.
- Deriche R. Using Canny's criteria to derive a recursively implemented optimal edge detector / R. Deriche // Int. J. Computer Vision .− 1987 .− Vol. 1 .− P. 167–187.
- Duda R.O. Use Of The Hough Trasformtion To Detect Lines And Curves In Pictures / Richard O. Duda, Peter E. Hart // The Communications of ACM .− 1972 .− Vol 15, No. 1 .− P. 11-15.
- Fisher, Perkins, Walker & Wolfart (2003). "Spatial Filters - Laplacian of Gaussian". Retrieved 2010-09-13 : [Electronic resource] .– http://homepages.inf.ed.ac.uk/rbf/HIPR2/log.htm.
- Prewitt J.M.S. Object Enhancement and Extraction / J.M.S. Prewitt // Picture processing and Psychopictorics .– NY:Academic Press,1970 .– P. 75-149
- Guil N. A fast Hough transform for segment detection, Image Processing / N. Guil, J. Villalba, Zapata // IEEE Transactions .− Nov 1995 .− P. 1541–1548.
- Rad Ali A. Fast Circle Detection Using Gradient Pair Vectors / Ali Ajdari Rad, Karim Faez, Navid Qaragozlou // Proc. VIIth Digital Image Computing .− Sydney, Australia, 2003.− P. 879-887.
- Sobel vs. Prewitt Masks for Edge Detection: [Electronic resource] .– http://the-evan.com/files/eel5820/project%2004/eel5802_pr04-05_turner_evan.pdf.
- Trajkovich M. Fast corner detection / M. Trajkovich, M. Handley // Image and Vision Computing .−1998 .− 16 .− P. 75-87.
- Ziou D, Tabbone S. Edge Detection Techniques - An Overview: [Electronic resource] .– http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.27.1821&rep=rep1&type=pdf
- Введение в контурный анализ / Я.А. Фурман, А.В. Кревецкий, А.К. Передреев и др.; Под ред. Я.А. Фурмана .− М.: ФИЗМАТЛИТ, 2003 .− 392 с.
- Гонсалес Р. Цифровая обработка изображений / Р. Гонсалес, Р. Вудс . – М.: Техносфера, 2005 .– 1070 с.
- Гонсалес Р. Цифровая обработка изображений в среде MATLAB/ Р. Гонсалес, Р. Вудс, С. Эддингс . – М.: Техносфера, 2006 .– 616 с.
- Денисюк В. С. Применение и оптимизация преобразования Хафа для поиска объектов на изображении / В.С. Денисюк // Международный конгресс по информатике: информационные системы и технологии: материалы международного научного конгресса 31 окт.– 3 нояб. 2011 г. .− Минск: БГУ, 2011.− Ч. 2.– C. 162-165.
- Лигун А.О. ALLDocument – технологія нового покоління для збереження, передачі та відображення електронних документів / А.О. Лигун, О.О. Шумейко, Д.В. Тимошенко // Вісник Східноукраїнського національного університету імені Володимира Даля .− 2006 .− №9 (103) Частина 1 .− C. 83-85.
- Лигун А.О. Про побудову майже інтерполяційних сплайнів Без’є / А.О. Лигун, О.О. Шумейко, Д.В. Тимошенко // Актуальні проблеми автоматизації та інформаційних технологій. Збірник наукових праць .– Дніпропетровськ, 2008 .– Том 12 .– С. 125-133.
- Лигун А.А. Локализация и формирование линий на изображении / А.А. Лигун, А.А. Шумейко, Д.В. Тимошенко // Системные технологии. Региональный межвузовский сборник научных трудов .− Днепропетровск, 2007 .− № 3(50) .− С. 5-14.
- Лигун А.А. Асимптотические методы восстановления кривых / А.А.Лигун, А.А.Шумейко .— К.: Изд. Института математики НАН Украины, 1997 .— 358 с.
- Прэтт У. Цифровая обработка зображений. Кн. 2 / У. Прэтт .− М.: Мир, 1982 .− 480 с.
- Роджерс Д. Математические основы машинной графики / Д. Роджерс, Дж. Адамс .– М.: Мир,2001 .– 357 c.
- Ту Дж. Принципы распознавания образов / Дж. Ту, Р. Гонсалес .− М., 1978 .− 410 с.